Mint tudjuk, a felügyelt gépi tanulási algoritmus nagyjából regressziós és osztályozási algoritmusokba sorolható. A regressziós algoritmusokban megjósoltuk a folytonos értékek kimenetét, de a kategorikus értékek előrejelzéséhez osztályozási algoritmusokra van szükség.

Mi az osztályozási algoritmus?

Az osztályozási algoritmus egy felügyelt tanulási technika, amely az új megfigyelések kategóriájának azonosítására szolgál a betanítási adatok alapján. Az osztályozásban a program tanul az adott adathalmazból vagy megfigyelésekből, majd az új megfigyeléseket több osztályba vagy csoportba sorolja. Mint például, Igen vagy nem, 0 vagy 1, Spam vagy nem spam, macska vagy kutya, stb. Az osztályokat célként/címkéként vagy kategóriáként hívhatjuk.

latex asztal

A regresszióval ellentétben az osztályozás kimeneti változója egy kategória, nem pedig egy érték, például „Zöld vagy Kék”, „gyümölcs vagy állat” stb. Mivel az osztályozási algoritmus egy felügyelt tanulási technika, ezért címkézett bemeneti adatokat vesz fel, amelyek azt jelenti, hogy bemenetet tartalmaz a megfelelő kimenettel.

Az osztályozási algoritmusban egy diszkrét kimeneti függvény (y) van leképezve az (x) bemeneti változóra.

 y=f(x), where y = categorical output 

Az ML osztályozási algoritmus legjobb példája az E-mail Spam Detector .

Az osztályozási algoritmus fő célja egy adott adathalmaz kategóriájának azonosítása, és ezek az algoritmusok elsősorban a kategorikus adatok kimenetének előrejelzésére szolgálnak.

Az osztályozási algoritmusok jobban megérthetők az alábbi diagram segítségével. Az alábbi diagramon két osztály található, az A és a B osztály. Ezek az osztályok hasonló tulajdonságokkal rendelkeznek, és különböznek a többi osztálytól.

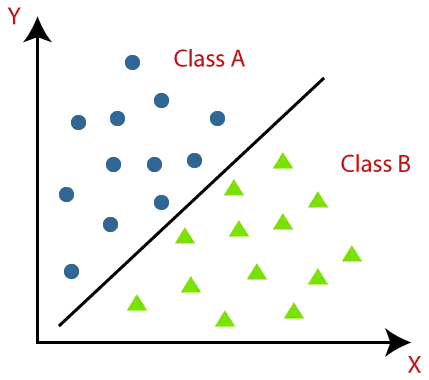
Az osztályozást egy adatkészleten megvalósító algoritmust osztályozónak nevezzük. Kétféle osztályozás létezik:

Bináris osztályozó:Ha az osztályozási problémának csak két lehetséges kimenetele van, akkor bináris osztályozónak nevezzük.
Példák: IGEN vagy NEM, FÉRFI vagy NŐ, SPAM vagy NEM SPAM, MACSKA vagy KUTYA stb.Több osztályos osztályozó:Ha egy osztályozási problémának kettőnél több kimenetele van, akkor többosztályú osztályozónak nevezzük.
Példa: Terményfajták osztályozása, Zenefajták osztályozása.

Tanulók osztályozási problémákban:

Az osztályozási feladatokban kétféle tanuló van:

Lusta tanulók:A Lazy Learner először tárolja a képzési adatkészletet, és várja meg, amíg megkapja a tesztadatkészletet. Lusta tanuló esetén az osztályozás a képzési adatkészletben tárolt, leginkább kapcsolódó adatok alapján történik. Kevesebb időt vesz igénybe az edzés, de több idő az előrejelzésekhez.
Példa: K-NN algoritmus, esetalapú gondolkodásLelkes tanulók:A lelkes tanulók egy besorolási modellt dolgoznak ki egy képzési adatkészlet alapján, mielőtt megkapnák a tesztadatkészletet. A Lusta tanulókkal szemben az Eager Learner több időt vesz igénybe a tanulásban, és kevesebb időt vesz igénybe az előrejelzésben. Példa: Decision Trees, Na�ve Bayes, ANN.

Az ML osztályozási algoritmusok típusai:

Az osztályozási algoritmusok tovább oszthatók a Főleg két kategóriába:

Lineáris modellek
• Logisztikus regresszió
• Támogatja a vektoros gépeket
Nemlineáris modellek
• K-Legközelebbi szomszédok
• Kernel SVM
• Na�ne Bayes
• Döntési fa osztályozása
• Véletlenszerű erdőbesorolás

Megjegyzés: A fenti algoritmusokat a későbbi fejezetekben fogjuk megtanulni.

Az osztályozási modell értékelése:

Miután elkészült a modellünk, ki kell értékelni a teljesítményét; vagy osztályozási vagy regressziós modell. Tehát az osztályozási modell értékeléséhez a következő módszerek állnak rendelkezésünkre:

1. Naplóveszteség vagy keresztentrópia veszteség:

• Egy olyan osztályozó teljesítményének értékelésére szolgál, amelynek kimenete 0 és 1 közötti valószínűségi érték.
• Egy jó bináris osztályozási modellhez a log veszteség értékének 0 közelében kell lennie.
• A log veszteség értéke növekszik, ha a becsült érték eltér a tényleges értéktől.
• Az alacsonyabb log veszteség a modell nagyobb pontosságát jelenti.
• A bináris osztályozáshoz a keresztentrópia a következőképpen számítható ki:

 ?(ylog(p)+(1?y)log(1?p)) 

Ahol y = tényleges kimenet, p = előrejelzett kimenet.

2. Zavart mátrix:

• A zavaros mátrix egy mátrixot/táblázatot biztosít számunkra kimenetként, és leírja a modell teljesítményét.
• Hibamátrixként is ismert.
• A mátrix előrejelzési eredményekből áll, amelyek egy összegzett formában vannak, amelyekben összesen helyes és hibás előrejelzések vannak. A mátrix az alábbi táblázat szerint néz ki:

3. AUC-ROC görbe:

java webszolgáltatások

• A ROC görbe jelentése Vevő működési jellemzői görbe és az AUC jelentése Görbe alatti terület .
• Ez egy grafikon, amely az osztályozási modell teljesítményét mutatja különböző küszöbértékeken.
• A többosztályos osztályozási modell teljesítményének megjelenítéséhez az AUC-ROC görbét használjuk.
• A ROC-görbe a TPR-vel és az FPR-rel van ábrázolva, ahol a TPR (valós pozitív arány) az Y tengelyen, és az FPR (hamis pozitív arány) az X tengelyen.

Az osztályozási algoritmusok felhasználási esetei

Az osztályozási algoritmusok különböző helyeken használhatók. Az alábbiakban bemutatjuk az osztályozási algoritmusok néhány népszerű használati esetét:

• E-mail spam észlelése
• Beszédfelismerés
• A rákos daganatsejtek azonosítása.
• A gyógyszerek besorolása
• Biometrikus azonosítás stb.