Először is meg fogjuk érteni a bináris fa és bináris keresőfa külön-külön, majd megvizsgáljuk a bináris fa és a bináris keresőfa közötti különbségeket.
Mi az a bináris fa?
A Bináris fa egy
A bináris fa a következőképpen ábrázolható:
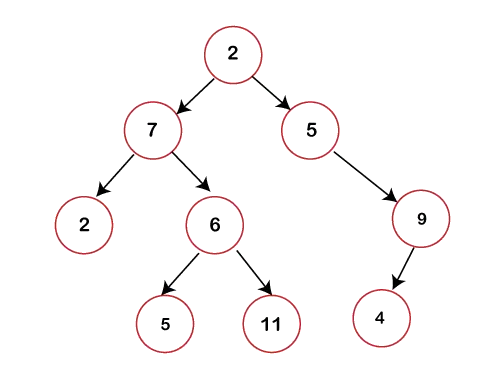
A fenti ábrán megfigyelhetjük, hogy minden csomópont legfeljebb 2 gyermeket tartalmaz. Ha valamelyik csomópont nem tartalmaz bal vagy jobb oldali gyermeket, akkor a mutató értéke az adott gyermekhez képest NULL lesz.
A bináris fában használt alapvető terminológiák a következők:
Egy bináris fában van egy fa, amelyet a néven ismerünk tökéletes bináris fa . Ez egy fa, amelyben az összes belső csomópontnak két csomópontot kell tartalmaznia, és az összes levélcsomópontnak azonos mélységben kell lennie. Tökéletes bináris fa esetén a bináris fában található csomópontok teljes száma a következő egyenlettel számítható ki:
n = 2m+1-1
ahol n a csomópontok száma, m a csomópont mélysége.
Mi az a bináris keresőfa?
A Bináris keresőfa egy fa, amely bizonyos sorrendet követ az elemek elrendezésében, míg a bináris fa nem követ semmilyen sorrendet. A bináris keresési fában a bal oldali csomópont értékének kisebbnek kell lennie, mint a szülőcsomóponté, és a jobb oldali csomópont értékének nagyobbnak kell lennie, mint a szülőcsomóponté.
Ismerjük meg a bináris keresőfa fogalmát példákon keresztül.

A fenti ábrán megfigyelhetjük, hogy a gyökércsomópont értéke 15, ami nagyobb, mint a bal oldali részfa összes csomópontjának értéke. A gyökércsomópont értéke kisebb, mint a jobb oldali részfa összes csomópontjának értéke. Most áttérünk a gyökércsomópont bal gyermekére. 10 nagyobb, mint 8 és kisebb, mint 12; a Bináris keresőfa tulajdonságát is kielégíti. Most áttérünk a gyökércsomópont jobb gyermekére; a 20 érték nagyobb, mint 17 és kisebb, mint 25; a bináris keresőfa tulajdonságát is kielégíti. Ezért azt mondhatjuk, hogy a fent látható fa a bináris keresőfa.
Ha a fenti bináris fában a 12-t 16-ra változtatjuk, meg kell találnunk, hogy ez még mindig bináris keresőfa-e vagy sem.

A gyökércsomópont értéke 15, ami 10-nél nagyobb, de 16-nál kisebb, tehát nem felel meg a Bináris keresőfa tulajdonságának. Ezért ez nem egy bináris keresőfa.
Műveletek a bináris keresőfán
A bináris keresőfán beszúrási, törlési és keresési műveleteket végezhetünk. Nézzük meg, hogyan történik a keresés bináris keresésen. Az alábbiakban látható a bináris fa, amelyen el kell végeznünk a keresési műveletet:

Tegyük fel, hogy 10-et kell keresnünk a fenti bináris fában. A bináris keresés végrehajtásához figyelembe vesszük az összes egész számot egy rendezett tömbben. Először egy teljes listát hozunk létre a keresési mezőben, és az összes szám ott lesz a keresési területen. A keresési területet két mutató jelöli, azaz a kezdet és a vége. A fenti bináris fa tömbje a következőképpen ábrázolható

Először kiszámítjuk a középső elemet, és összehasonlítjuk a középső elemet a keresendő elemmel. A középső elemet n/2 segítségével számítjuk ki. n értéke 7; ezért a középső elem 15. A középső elem nem egyenlő a keresett elemmel, azaz 10.
Megjegyzés: Ha a keresett elem kisebb, mint a középső elem, akkor a keresés a bal felében történik; egyébként a keresés a jobb oldalon történik. Egyenlőség esetén az elem található.
Mivel a keresendő elem kisebb, mint a középső elem, így a keresés a bal oldali tömbön történik. Most a keresés a felére csökkent, amint az alább látható:

A bal oldali tömb középső eleme 10, ami megegyezik a keresett elemmel.
Időbeli összetettség
A bináris keresésben n elem van. Ha a középső elem nem egyenlő a keresett elemmel, akkor a keresési teret n/2-re csökkentjük, és a keresési teret n/2-vel csökkentjük, amíg meg nem találjuk az elemet. A teljes redukcióban, ha n-ről n/2-re lépünk n/4-re és így tovább, akkor log kell2n lépésben.
A bináris fa és a bináris keresési fa közötti különbségek

| Összehasonlítási alap | Bináris fa | Bináris keresőfa |
|---|---|---|
| Meghatározás | A bináris fa egy nemlineáris adatstruktúra, amelyben egy csomópontnak legfeljebb két gyermeke lehet, azaz egy csomópontnak 0, 1 vagy legfeljebb két gyermeke lehet. A bináris keresési fa egy rendezett bináris fa, amelyben bizonyos sorrendet követnek a csomópontok rendszerezése egy fában. | |
| Szerkezet | A bináris fa szerkezete az, hogy az első csomópontot vagy a legfelső csomópontot gyökércsomópontnak nevezzük. A bináris fa minden csomópontja tartalmazza a bal és a jobb oldali mutatót. A bal mutató a bal oldali részfa címét tartalmazza, míg a jobb oldali a jobb oldali részfa címét. | A bináris keresőfa a bináris fa azon típusainak egyike, amelyeknél a bal oldali részfa összes csomópontjának értéke kisebb vagy egyenlő a gyökércsomóponttal, és a jobb oldali részfa összes csomópontjának értéke nagyobb vagy egyenlő, mint a gyökércsomópont értéke. |
| Tevékenységek | A bináris fán megvalósítható műveletek a beszúrás, törlés és bejárás. | A bináris keresőfák olyan rendezett bináris fák, amelyek gyors beszúrást, törlést és keresést biztosítanak. A keresések főként bináris keresést valósítanak meg, mivel az összes kulcs rendezési sorrendben van elrendezve. |
| típusok | A bináris fa négy típusa a teljes bináris fa, a teljes bináris fa, a tökéletes bináris fa és a kiterjesztett bináris fa. | Különféle típusú bináris keresőfák léteznek, például AVL-fák, Splay-fák, Tango-fák stb. |
