Ebben a cikkben a bináris keresési fát tárgyaljuk. Ez a cikk nagyon hasznos és informatív lesz a műszaki háttérrel rendelkező hallgatók számára, mivel ez a kurzusuk fontos témája.
Mielőtt közvetlenül a bináris keresőfára lépne, először nézzük meg a fa rövid leírását.
Mi az a fa?
A fa egyfajta adatstruktúra, amely az adatok hierarchikus formában történő megjelenítésére szolgál. Meghatározható objektumok vagy entitások gyűjteményeként, amelyeket csomópontoknak neveznek, és amelyek összekapcsolódnak egy hierarchia szimulálására. A fa egy nemlineáris adatstruktúra, mivel a fában lévő adatok nem lineárisan vagy szekvenciálisan kerülnek tárolásra.
Most kezdjük a témával, a Bináris keresés fával.
arraylist.sort
Mi az a bináris keresőfa?
A bináris keresőfa bizonyos sorrendet követ az elemek elrendezésében. A bináris keresési fában a bal oldali csomópont értékének kisebbnek kell lennie, mint a szülőcsomóponté, és a jobb oldali csomópont értékének nagyobbnak kell lennie, mint a szülőcsomóponté. Ezt a szabályt a rendszer rekurzívan alkalmazza a gyökér bal és jobb oldali részfáira.
Ismerjük meg a bináris keresőfa fogalmát egy példán keresztül.
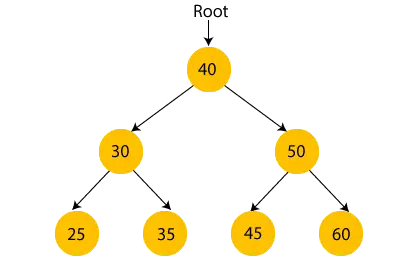
A fenti ábrán megfigyelhetjük, hogy a gyökércsomópont 40, és a bal oldali részfa összes csomópontja kisebb, mint a gyökércsomópont, a jobb oldali részfa összes csomópontja pedig nagyobb, mint a gyökércsomópont.
Hasonlóképpen láthatjuk, hogy a gyökércsomópont bal gyermeke nagyobb, mint a bal gyermeke, és kisebb, mint a jobb gyermeke. Tehát a bináris keresőfa tulajdonságát is kielégíti. Ezért azt mondhatjuk, hogy a fenti képen látható fa egy bináris keresőfa.
Tegyük fel, hogy ha a fenti fában megváltoztatjuk a 35-ös csomópont értékét 55-re, akkor ellenőrizzük, hogy a fa bináris keresési fa lesz-e vagy sem.
hány billentyű van a billentyűzeteken

A fenti fában a gyökércsomópont értéke 40, ami nagyobb, mint a bal gyermeke 30, de kisebb, mint a 30 jobb gyermeke, azaz 55. Tehát a fenti fa nem elégíti ki a Bináris keresőfa tulajdonságát. Ezért a fenti fa nem bináris keresőfa.
A bináris keresőfa előnyei
- Egy elem keresése a Bináris keresőfában egyszerű, mivel mindig van egy tippünk, hogy melyik részfában van a kívánt elem.
- A tömbökhöz és a hivatkozott listákhoz képest a beillesztési és törlési műveletek gyorsabbak a BST-ben.
Példa bináris keresőfa létrehozására
Most pedig lássuk a bináris keresési fa létrehozását egy példa segítségével.
Tegyük fel, hogy az adatelemek - 45, 15, 79, 90, 10, 55, 12, 20, 50
- Először is be kell illesztenünk Négy öt a fába, mint a fa gyökerébe.
- Ezután olvassa el a következő elemet; ha kisebb, mint a gyökércsomópont, illessze be a bal oldali részfa gyökereként, és lépjen a következő elemre.
- Ellenkező esetben, ha az elem nagyobb, mint a gyökércsomópont, akkor szúrja be a jobb oldali részfa gyökereként.
Most nézzük meg a bináris keresési fa létrehozásának folyamatát az adott adatelem használatával. A BST létrehozásának folyamata az alábbiakban látható -
1. lépés – Helyezze be a 45-öt.

2. lépés – Helyezze be a 15-öt.
Mivel a 15 kisebb, mint 45, ezért illessze be a bal oldali részfa gyökércsomópontjaként.

3. lépés – Szúrja be a 79-et.
Mivel a 79 nagyobb, mint 45, illessze be a jobb oldali részfa gyökércsomópontjaként.
k legközelebbi szomszéd algoritmus

4. lépés – Helyezze be a 90-et.
A 90 nagyobb, mint 45 és 79, ezért a 79 jobb oldali részfájaként kerül beillesztésre.

5. lépés – Helyezze be a 10-et.
A 10 kisebb, mint 45 és 15, ezért a 15-ös bal oldali részfaként lesz beszúrva.

6. lépés – Illessze be az 55-öt.
Az 55 nagyobb, mint 45 és kisebb, mint 79, ezért a 79 bal oldali részfájaként lesz beszúrva.

7. lépés – Helyezze be a 12-t.
A 12 kisebb, mint 45 és 15, de nagyobb, mint 10, ezért a 10 jobb oldali részfájaként kerül beillesztésre.

8. lépés – Helyezze be a 20-at.
A 20 kisebb, mint 45, de nagyobb, mint 15, ezért a 15-ös jobb oldali részfaként lesz beszúrva.
véletlenszerű sorrend sql-ben

9. lépés – Helyezze be az 50-et.
Az 50 nagyobb, mint 45, de kisebb, mint 79 és 55. Tehát az 55-ös bal oldali részfaként lesz beszúrva.

Ezzel a bináris keresőfa létrehozása befejeződött. Ezek után térjünk át a Bináris keresőfán végrehajtható műveletek felé.
A bináris keresőfán beszúrási, törlési és keresési műveleteket végezhetünk.
Nézzük meg, hogyan történik a keresés egy bináris keresési fán.
Keresés a bináris keresési fában
A keresés egy adott elem vagy csomópont megtalálását vagy helyének meghatározását jelenti egy adatszerkezetben. A bináris keresési fában a csomópontok keresése egyszerű, mivel a BST elemei meghatározott sorrendben vannak tárolva. A csomópontok keresésének lépései a bináris keresés fában a következők:
- Először hasonlítsa össze a keresendő elemet a fa gyökérelemével.
- Ha a gyökér egyezik a cél elemmel, akkor adja vissza a csomópont helyét.
- Ha nem egyezik, akkor ellenőrizze, hogy az elem kisebb-e, mint a gyökérelem, ha kisebb, mint a gyökérelem, akkor lépjen a bal oldali részfára.
- Ha nagyobb, mint a gyökérelem, akkor lépjen a jobb oldali részfára.
- Ismételje meg a fenti eljárást rekurzív módon, amíg meg nem találja az egyezést.
- Ha az elem nem található vagy nem szerepel a fában, akkor adja vissza a NULL értéket.
Most értsük meg a bináris fában való keresést egy példa segítségével. A fent kialakított bináris keresőfát vesszük. Tegyük fel, hogy meg kell találnunk a 20-as csomópontot az alábbi fából.
1. lépés:

2. lépés:

3. lépés:

Most nézzük meg az algoritmust, amellyel egy elemet kereshet a bináris keresési fában.
ha else utasítások java
Algoritmus egy elem keresésére a bináris keresési fában
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Kimenet
A fenti kód végrehajtása után a kimenet a következő lesz:

Szóval ennyi a cikkről. Reméljük, hogy a cikk hasznos és informatív lesz az Ön számára.
