A számítógépek feltalálása óta az emberek ezt a kifejezést használják. Adat ' a továbbított vagy tárolt számítógépes információkra utal. Vannak azonban olyan adatok, amelyek rendeléstípusoknál is léteznek. Az adatok lehetnek számok vagy papírra írt szövegek, elektronikus eszközök memóriájában tárolt bitek és bájtok formájában, vagy az ember elméjében tárolt tények. Ahogy a világ korszerűsödni kezdett, ezek az adatok mindenki mindennapi életének jelentős részévé váltak, és a különféle megvalósítások lehetővé tették számukra, hogy eltérő módon tárolják őket.

Adat tények és számok gyűjteménye, vagy meghatározott formátumú értékek vagy értékek halmaza, amely egyetlen tételérték-készletre utal. Az adatelemek ezután altételekbe kerülnek besorolásra, amelyek az elemek azon csoportja, amelyek nem ismertek az elem egyszerű elsődleges formájaként.

Vegyünk egy példát, ahol egy alkalmazott neve három alelemre bontható: Első, Középső és Utolsó. Az alkalmazotthoz rendelt azonosító azonban általában egyetlen tételnek minősül.

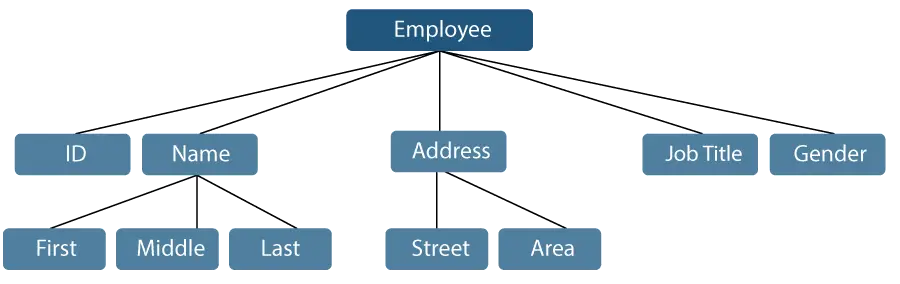
1.ábra: Adatelemek ábrázolása

A fent említett példában az olyan elemek, mint az azonosító, életkor, nem, első, középső, utolsó, utca, helység stb., elemi adatelemek. Ezzel szemben a Név és a Cím csoport adatelemek.

Mi az adatstruktúra?

Adatstruktúra a számítástechnika egyik ága. Az adatstruktúra tanulmányozása lehetővé teszi számunkra, hogy megértsük az adatok szerveződését és az adatáramlás kezelését bármely folyamat vagy program hatékonyságának növelése érdekében. Az adatstruktúra egy sajátos módja az adatok tárolásának és rendszerezésének a számítógép memóriájában, hogy ezek az adatok könnyen visszakereshetők és a jövőben szükség esetén hatékonyan felhasználhatók legyenek. Az adatokat többféleképpen lehet kezelni, például egy adott adatszervezet logikai vagy matematikai modelljét adatszerkezetnek nevezzük.

Egy adott adatmodell hatóköre két tényezőtől függ:

1. Először is, eléggé be kell tölteni a struktúrába ahhoz, hogy tükrözze az adatok és egy valós objektum határozott korrelációját.
2. Másodszor, a formálásnak olyan egyszerűnek kell lennie, hogy szükség esetén alkalmazkodni lehessen az adatok hatékony feldolgozásához.

Néhány példa az adatstruktúrákra: tömbök, linkelt listák, verem, sor, fák stb. Az adatstruktúrákat széles körben használják a számítástechnika szinte minden területén, például a fordítótervezésben, az operációs rendszerekben, a grafikában, a mesterséges intelligenciában és még sok másban.

Az adatstruktúrák számos számítástechnikai algoritmus fő részét képezik, mivel lehetővé teszik a programozók számára az adatok hatékony kezelését. Döntő szerepet játszik egy program vagy szoftver teljesítményének javításában, mivel a szoftver fő célja a felhasználó adatainak lehető leggyorsabb tárolása és visszakeresése.

css megjegyzés

Az adatstruktúrákhoz kapcsolódó alapvető terminológiák

Az adatstruktúrák bármely szoftver vagy program építőkövei. A megfelelő adatstruktúra kiválasztása egy program számára rendkívül nagy kihívást jelent egy programozó számára.

A következőkben néhány alapvető terminológiát használunk, amikor az adatstruktúrákról van szó:

Adat:Az adatokat elemi értékként vagy értékgyűjteményként definiálhatjuk. Például a Munkavállaló neve és azonosítója a Munkavállalóval kapcsolatos adat.Adatelemek:Az Egyetlen értékegységet adatelemnek nevezzük.Csoportos elemek:Az alárendelt adatelemekkel rendelkező adatelemeket csoportelemeknek nevezzük. Például egy alkalmazott neve tartalmazhat kereszt-, közép- és vezetéknevet.Alapelemek:Azokat az adatelemeket, amelyeket nem lehet alelemekre osztani, elemi elemeknek nevezzük. Például egy alkalmazott azonosítója.Entitás és attribútum:Bizonyos objektumok egy osztályát egy entitás képviseli. Különböző attribútumokból áll. Minden attribútum az adott entitás sajátos tulajdonságát szimbolizálja. Például,

A hasonló attribútumokkal rendelkező entitások an Entitáskészlet . Egy entitáskészlet minden attribútumának van egy értéktartománya, az összes lehetséges érték halmaza, amely az adott attribútumhoz rendelhető.

Az „információ” kifejezést időnként olyan adatokra használják, amelyek jelentéses vagy feldolgozott adatok adott attribútumai vannak.

Terület:Az entitás attribútumait szimbolizáló egyetlen elemi információegységet mezőnek nevezzük.Rekord:Különféle adatelemek gyűjteménye rekordként ismert. Például, ha az alkalmazotti entitásról beszélünk, akkor annak neve, azonosítója, címe és beosztása csoportosítható az alkalmazott rekordjának kialakításához.Fájl:Egy entitástípus különböző rekordjainak gyűjteménye fájlként ismert. Például, ha 100 alkalmazottról van szó, akkor a kapcsolódó fájlban 25 rekord lesz, amelyek minden alkalmazottról adatokat tartalmaznak.

Az adatszerkezetek szükségességének megértése

Mivel az alkalmazások egyre összetettebbek, és az adatok mennyisége napról napra növekszik, ami problémákhoz vezethet az adatkereséssel, a feldolgozási sebességgel, a többszörös kérés kezelésével és még sok mással kapcsolatban. Az adatstruktúrák különböző módszereket támogatnak az adatok hatékony szervezésére, kezelésére és tárolására. A Data Structures segítségével könnyedén bejárhatjuk az adatelemeket. Az adatstruktúrák hatékonyságot, újrafelhasználhatóságot és absztrakciót biztosítanak.

Miért érdemes adatstruktúrákat tanulnunk?

1. Az adatstruktúrák és az algoritmusok a számítástechnika két kulcsfontosságú aspektusa.
2. Az adatstruktúrák lehetővé teszik az adatok rendszerezését és tárolását, míg az algoritmusok lehetővé teszik az adatok értelmes feldolgozását.
3. Az adatstruktúrák és algoritmusok megtanulása segít abban, hogy jobb programozókká váljunk.
4. Hatékonyabb és megbízhatóbb kódot tudunk majd írni.
5. A problémákat is gyorsabban és hatékonyabban tudjuk majd megoldani.

Az adatstruktúrák céljainak megértése

Az adatstruktúrák két egymást kiegészítő célt teljesítenek:

java arraylist rendezve

Helyesség:Az adatstruktúrákat úgy tervezték, hogy az érdeklődési területtől függően mindenféle bemenet esetén megfelelően működjenek. Egyszóval a helyesség az Adatstruktúra elsődleges célja, amely mindig azoktól a problémáktól függ, amelyeket az Adatstruktúra megoldani hivatott.Hatékonyság:Az adatstruktúráknak is hatékonynak kell lenniük. Gyorsan kell feldolgoznia az adatokat anélkül, hogy sok számítógépes erőforrást (például memóriaterületet) használna. Valós idejű állapotban az adatstruktúra hatékonysága kulcsfontosságú tényező a folyamat sikerének és kudarcának meghatározásában.

Az adatstruktúrák néhány fő jellemzőjének megértése

Az adatstruktúrák néhány fontos jellemzője:

Robusztusság:Általában minden számítógép-programozó arra törekszik, hogy olyan szoftvert állítson elő, amely minden lehetséges bemenethez megfelelő kimenetet ad, valamint hatékony végrehajtást minden hardverplatformon. Az ilyen típusú robusztus szoftvereknek érvényes és érvénytelen bemeneteket is kezelniük kell.Alkalmazkodhatóság:Az olyan szoftveralkalmazások építése, mint a webböngészők, szövegszerkesztők és internetes keresőmotorok, hatalmas szoftverrendszereket tartalmaznak, amelyek sok éven át megfelelő és hatékony működést vagy végrehajtást igényelnek. Ráadásul a szoftverek a feltörekvő technológiák vagy a folyamatosan változó piaci feltételek miatt fejlődnek.Újrahasználhatóság:Az olyan funkciók, mint az újrafelhasználhatóság és az adaptálhatóság, kéz a kézben járnak. Köztudott, hogy a programozónak sok erőforrásra van szüksége bármilyen szoftver elkészítéséhez, így ez költséges vállalkozás. Ha azonban a szoftvert újrafelhasználható és adaptálható módon fejlesztik, akkor a legtöbb jövőbeni alkalmazásban alkalmazható lesz. Így a minőségi adatszerkezetek végrehajtásával újrafelhasználható szoftverek építhetők fel, ami költséghatékonynak és időtakarékosnak tűnik.

Adatstruktúrák osztályozása

Az adatstruktúra olyan változók strukturált halmazát adja meg, amelyek különféle módon kapcsolódnak egymáshoz. Ez egy olyan programozási eszköz alapját képezi, amely jelzi az adatelemek közötti kapcsolatot, és lehetővé teszi a programozók számára az adatok hatékony feldolgozását.

Az adatstruktúrákat két kategóriába sorolhatjuk:

1. Primitív adatstruktúra
2. Nem primitív adatstruktúra

A következő ábra az adatstruktúrák különböző osztályozásait mutatja be.

2. ábra: Adatstruktúrák osztályozása

Primitív adatszerkezetek

Primitív adatszerkezeteka számokból és a megjelenő karakterekből álló adatstruktúrák beépített programokba.
1. Ezeket az adatstruktúrákat gépi szintű utasításokkal lehet közvetlenül manipulálni vagy működtetni.
2. Az alapvető adattípusok, mint pl Egész szám, úszó, karakter , és Boolean a Primitív Adatstruktúrák alá tartoznak.
3. Ezeket az adattípusokat más néven Egyszerű adattípusok , mivel olyan karaktereket tartalmaznak, amelyeket nem lehet tovább osztani

Nem primitív adatstruktúrák

Nem primitív adatstruktúrákazok az adatstruktúrák, amelyek a Primitív Adatstruktúrákból származnak.
1. Ezeket az adatstruktúrákat nem lehet közvetlenül gépi szintű utasításokkal manipulálni vagy működtetni.
2. Ezeknek az adatstruktúráknak a középpontjában egy olyan adatelem-készlet kialakítása áll, amely vagy homogén (azonos adattípus) ill heterogén (különböző adattípusok).
3. Az adatok szerkezete és elrendezése alapján ezeket az adatstruktúrákat két alkategóriára oszthatjuk -
   1. Lineáris adatstruktúrák
   2. Nemlineáris adatstruktúrák

Lineáris adatstruktúrák

Az adatszerkezetet, amely megőrzi az adatelemei közötti lineáris kapcsolatot, Lineáris adatszerkezetnek nevezzük. Az adatok elrendezése lineárisan történik, ahol az első és az utolsó adatelem kivételével minden elem az utódokból és az elődekből áll. Ez azonban nem feltétlenül igaz a memória esetében, mivel az elrendezés nem feltétlenül szekvenciális.

A memóriafoglalás alapján a lineáris adatstruktúrákat további két típusra osztják:

Statikus adatszerkezetek:A rögzített méretű adatstruktúrákat statikus adatstruktúráknak nevezzük. Ezeknek az adatstruktúráknak a memóriáját a fordítóidőben foglalják le, és méretüket a felhasználó nem tudja megváltoztatni a fordítás után; a bennük tárolt adatok azonban módosíthatók.
A Sor a Static Data Structure legjobb példája, mivel fix méretűek, és adatai később módosíthatók.Dinamikus adatstruktúrák:A dinamikus méretű adatstruktúrákat dinamikus adatstruktúráknak nevezzük. Ezeknek az adatstruktúráknak a memóriája a futási időben le van foglalva, és méretük a kód futási ideje alatt változik. Ezen túlmenően a felhasználó a kód futási idejében módosíthatja a méretet, valamint az ezekben az adatstruktúrákban tárolt adatelemeket.
Hivatkozott listák, halmok , és Frakk gyakori példái a dinamikus adatstruktúráknak

Lineáris adatstruktúrák típusai

Az alábbiakban felsoroljuk az általunk általában használt lineáris adatstruktúrákat:

1. Tömbök

An Sor egy olyan adatstruktúra, amely több, azonos típusú adatelemet egyetlen változóba gyűjt. Ahelyett, hogy ugyanazon adattípusok több értékét külön változónévben tárolnánk, az összeset egy változóban tárolhatjuk. Ez az állítás nem jelenti azt, hogy bármely programban ugyanannak az adattípusnak az összes értékét egy adott adattípusú tömbbe kell egyesítenünk. De gyakran előfordulnak olyan esetek, amikor ugyanazon adattípusok bizonyos változói egy tömbnek megfelelő módon kapcsolódnak egymáshoz.

A tömb olyan elemek listája, ahol minden elemnek egyedi helye van a listában. A tömb adatelemei ugyanazon a változónéven osztoznak; azonban mindegyik más indexszámot hordoz, amelyet alsó indexnek neveznek. A listából bármelyik adatelemet elérhetjük a listában való elhelyezkedése segítségével. Így a tömbök legfontosabb jellemzője, hogy az adatokat összefüggő memóriahelyeken tárolják, lehetővé téve a felhasználók számára a tömb adatelemeinek áthaladását a megfelelő indexek segítségével.

3. ábra. Egy tömb

A tömbök különböző típusokba sorolhatók:

Egydimenziós tömb:A csak egy sor adatelemet tartalmazó tömb egydimenziós tömb néven ismert. Tárolása növekvő tárolóhelyen történik.Kétdimenziós tömb:Az adatelemek több sorából és oszlopából álló tömböt kétdimenziós tömbnek nevezzük. Mátrix néven is ismert.Többdimenziós tömb:A többdimenziós tömböt tömbök tömbjeként definiálhatjuk. A többdimenziós tömbök nincsenek két indexhez vagy két dimenzióhoz kötve, mivel szükség szerint annyi indexet tartalmazhatnak.

A tömb néhány alkalmazása:

1. Az azonos adattípushoz tartozó adatelemek listáját tárolhatjuk.
2. A tömb más adatszerkezetek kiegészítő tárolójaként működik.
3. A tömb segít a rögzített szám bináris fa adatelemeinek tárolásában is.
4. A tömb mátrixok tárolójaként is működik.

2. Hivatkozott listák

A Linkelt lista egy másik példa egy lineáris adatszerkezetre, amelyet adatelemek gyűjteményének dinamikus tárolására használnak. Ebben az adatstruktúrában az adatelemeket a csomópontok képviselik, amelyek hivatkozásokkal vagy mutatókkal vannak összekapcsolva. Minden csomópont két mezőt tartalmaz, az információs mező a tényleges adatokat, a mutató mező pedig a lista következő csomópontjainak címét tartalmazza. A hivatkozott lista utolsó csomópontjának mutatója egy null mutatóból áll, mivel semmire mutat. A tömböktől eltérően a felhasználó dinamikusan állíthatja be a csatolt lista méretét a követelményeknek megfelelően.

4. ábra. Egy linkelt lista

A linkelt listák különböző típusokba sorolhatók:

Egyedül linkelt lista:Az egyszeresen linkelt lista a linkelt lista leggyakoribb típusa. Minden csomópont rendelkezik adatokkal és egy mutatómezővel, amely a következő csomópont címét tartalmazza.Duplán linkelt lista:A Duplán linkelt lista egy információs mezőből és két mutatómezőből áll. Az információs mező tartalmazza az adatokat. Az első mutatómező az előző csomópont címét tartalmazza, míg egy másik mutatómező a következő csomópontra való hivatkozást tartalmazza. Így mindkét irányba haladhatunk (hátra és előre is).Körlevél linkelt lista:A körkörös linkelt lista hasonló az egyszeresen linkelt listához. Az egyetlen lényeges különbség az, hogy az utolsó csomópont tartalmazza az első csomópont címét, ami körkörös hurkot képez a Circular Linked List-ben.

A linkelt listák néhány alkalmazása:

1. A linkelt listák segítenek nekünk előre meghatározott méretű veremeket, sorokat, bináris fákat és grafikonokat megvalósítani.
2. Az operációs rendszer dinamikus memóriakezelési funkcióját is megvalósíthatjuk.
3. A csatolt listák lehetővé teszik a matematikai műveletek polinomiális megvalósítását is.
4. A Circular Linked List segítségével olyan operációs rendszereket vagy alkalmazási funkciókat valósíthatunk meg, amelyek körbejárják a feladatok végrehajtását.
5. A kör alakú linkelt lista a diavetítésben is hasznos, ahol a felhasználónak vissza kell térnie az első diához az utolsó dia bemutatása után.
6. A Duplán linkelt listát arra használják, hogy előre és hátra gombokat alkalmazzanak a böngészőben, hogy előre és hátra mozogjanak a webhely megnyitott oldalain.

3. Stack

A Kazal egy Lineáris adatstruktúra, amely követi a LIFO (Last In, First Out) elv, amely lehetővé teszi az olyan műveleteket, mint a beszúrás és a törlés a verem egyik végéről, azaz a tetejéről. A veremeket egymás melletti memória, egy tömb, valamint a nem szomszédos memória, a Linked List segítségével lehet megvalósítani. A Stacks valós példái a könyvhalmok, a kártyapakli, a pénzhalmok és még sok más.

5. ábra. A Stack valós példája

A fenti ábra egy halom valós példáját mutatja, ahol a műveleteket csak az egyik végéről hajtják végre, például új könyvek behelyezését és eltávolítását a verem tetejéről. Ez azt jelenti, hogy a verembe való beszúrás és törlés csak a verem tetejéről történhet. Egyszerre csak a Stack tetejét érhetjük el.

Az elsődleges műveletek a veremben a következők:

Nyom:Az új elem verembe való beillesztésére szolgáló műveletet Push műveletnek nevezzük.Pop:Az elemek veremből való eltávolítására vagy törlésére szolgáló műveletet Pop műveletnek nevezik.

6. ábra. Egy verem

A Stack néhány alkalmazása:

1. A verem ideiglenes tárolási struktúraként használható rekurzív műveletekhez.
2. A verem segédtároló struktúraként is használható függvényhívásokhoz, beágyazott műveletekhez és elhalasztott/halasztott funkciókhoz.
3. A Stacks segítségével kezelhetjük a függvényhívásokat.
4. A veremeket a különböző programozási nyelvek aritmetikai kifejezéseinek kiértékelésére is használják.
5. A veremek az infix kifejezések postfix kifejezésekké alakításában is hasznosak.
6. A veremek segítségével ellenőrizhetjük a kifejezés szintaxisát a programozási környezetben.
7. A Stacks segítségével párosíthatjuk a zárójeleket.
8. A veremekkel megfordíthatunk egy karakterláncot.
9. A veremek hasznosak a visszalépésen alapuló problémák megoldásában.
10. Használhatjuk a Stacks-et a mélységi kereséshez gráf- és fabejárásban.
11. A veremeket az operációs rendszer funkcióiban is használják.
12. A veremeket az UNDO és REDO funkciók is használják szerkesztéskor.

4. Farok

hogyan szünteted meg a kijelölést a gimpben

A Sor a veremhez hasonló lineáris adatstruktúra, amely bizonyos korlátozásokkal rendelkezik az elemek beszúrására és törlésére vonatkozóan. Egy elem beszúrása a sorba az egyik végén, az eltávolítás pedig a másik vagy ellentétes végén történik. Ebből arra következtethetünk, hogy a Queue adatstruktúra a FIFO (First In, First Out) elvet követi az adatelemek manipulálásához. A sorok megvalósítása tömbök, linkelt listák vagy veremek segítségével történhet. Néhány valós példa a Várólistákra: sor a jegypénztárnál, mozgólépcső, autómosó és még sok más.

7. ábra. Valós példa a sorra

A fenti kép egy mozijegy-számláló valós illusztrációja, amely segíthet megérteni azt a sort, ahol mindig az elsőként érkező vásárlót szolgálják ki először. Az utolsóként érkező vásárlót kétségtelenül utolsóként szolgálják ki. A sor mindkét vége nyitott, és különböző műveleteket hajthat végre. Egy másik példa egy élelmiszerpálya-sor, ahol az ügyfelet a hátulról helyezik be, míg a vevőt az elülső végén távolítják el, miután nyújtotta a kért szolgáltatást.

A sor elsődleges műveletei a következők:

Sorba állás:Egyes adatelemek beszúrását vagy hozzáadását a sorba sornak nevezik. Az elembeillesztés mindig a hátsó mutató segítségével történik.Sorból:Az adatelemek törlését vagy eltávolítását a várólistából dequeue-nak nevezzük. Az elem törlése mindig az elülső mutató segítségével történik.

8. ábra. Sor

A sorok néhány alkalmazása:

latex részleges származéka

1. A várólisták általában a Graphs szélességi keresési műveletében használatosak.
2. A várólisták az operációs rendszerek Job Scheduler műveleteiben is használatosak, például a billentyűzet puffersora a felhasználók által lenyomott billentyűk tárolására, valamint a nyomtatási puffersor a nyomtató által kinyomtatott dokumentumok tárolására.
3. A várólisták felelősek a CPU ütemezéséért, a Feladatütemezésért és a Lemezütemezésért.
4. A prioritási sorokat a böngésző fájlletöltési műveletei során használják.
5. A sorokat a perifériás eszközök és a CPU közötti adatátvitelre is használják.
6. A sorok felelősek a felhasználói alkalmazások által a CPU számára generált megszakítások kezeléséért is.

Nemlineáris adatstruktúrák

A nemlineáris adatstruktúrák olyan adatstruktúrák, amelyekben az adatelemek nincsenek egymás utáni sorrendben elrendezve. Itt az adatok beszúrása és eltávolítása nem valósítható meg lineárisan. Az egyes adatelemek között hierarchikus kapcsolat van.

A nemlineáris adatstruktúrák típusai

Az alábbiakban felsoroljuk az általunk általában használt nemlineáris adatstruktúrákat:

1. Fák

A fa egy nemlineáris adatstruktúra és egy olyan hierarchia, amely csomópontok gyűjteményét tartalmazza úgy, hogy a fa minden csomópontja egy értéket és egy hivatkozáslistát tárol a többi csomópontra (a „gyermekekre”).

A Tree adatstruktúra egy speciális módszer az adatok számítógépen történő elrendezésére és összegyűjtésére, hogy hatékonyabban hasznosítható legyen. Tartalmaz egy központi csomópontot, szerkezeti csomópontokat és élekkel összekapcsolt alcsomópontokat. Azt is mondhatjuk, hogy a fa adatszerkezete összefüggő gyökerekből, ágakból és levelekből áll.

9. ábra. Egy fa

A fákat különböző típusokra oszthatjuk:

Bináris fa:Az olyan fa adatszerkezetet, amelyben minden szülőcsomópontnak legfeljebb két gyermeke lehet, bináris fának nevezzük.Bináris keresőfa:A bináris keresőfa egy fa adatstruktúra, ahol könnyen karbantarthatunk egy rendezett számlistát.AVL fa:Az AVL-fa egy önkiegyensúlyozó bináris keresőfa, amelyben minden csomópont egy egyensúlytényezőként ismert extra információkat tart fenn, amelyek értéke -1, 0 vagy +1.B-fa:A B-fa az önkiegyensúlyozó bináris keresőfa egy speciális típusa, ahol minden csomópont több kulcsból áll, és kettőnél több gyermeke lehet.

A fák néhány alkalmazása:

1. A fák hierarchikus struktúrákat valósítanak meg számítógépes rendszerekben, például könyvtárakban és fájlrendszerekben.
2. A fákat a webhelyek navigációs szerkezetének megvalósítására is használják.
3. A Fák segítségével létrehozhatunk olyan kódot, mint a Huffman-kód.
4. A fák a játékalkalmazások döntéshozatalában is hasznosak.
5. A fák felelősek a prioritás alapú operációs rendszer-ütemezési funkciók prioritási sorainak megvalósításáért.
6. A fák felelősek a kifejezések és utasítások elemzéséért is a különböző programozási nyelvek fordítóiban.
7. A fák segítségével adatkulcsokat tárolhatunk az adatbázis-kezelő rendszer (DBMS) indexeléséhez.
8. A Spanning Trees lehetővé teszi a döntések irányítását a számítógépes és kommunikációs hálózatokban.
9. A fákat a mesterséges intelligencia (AI), a robotika és a videojáték alkalmazásokban megvalósított útkereső algoritmusban is használják.

2. Grafikonok

A gráf egy másik példa a nemlineáris adatszerkezetre, amely véges számú csomópontból vagy csúcsból és az ezeket összekötő élekből áll. A grafikonokat a valós világ problémáinak kezelésére használják, amelyekben a problématerületet hálózatként jelölik, például közösségi hálózatok, áramköri hálózatok és telefonhálózatok. Például egy gráf csomópontjai vagy csúcsai képviselhetnek egyetlen felhasználót a telefonhálózatban, míg az élek a köztük lévő telefonos kapcsolatot.

A G gráf adatstruktúrát olyan matematikai struktúrának tekintjük, amely V csúcsokból és E élek halmazából áll, az alábbiak szerint:

G = (V,E)

10. ábra. Egy grafikon

A fenti ábra egy gráfot ábrázol, amelynek hét csúcsa A, B, C, D, E, F, G, és tíz éle [A, B], [A, C], [B, C], [B, D], [B, E], [C, D], [D, E], [D, F], [E, F] és [E, G].

A csúcsok és élek helyzetétől függően a grafikonok különböző típusokba sorolhatók:

Null grafikon:Az üres élkészlettel rendelkező gráfot null gráfnak nevezzük.Triviális grafikon:A csak egy csúcsú gráfot triviális gráfnak nevezzük.Egyszerű grafikon:A sem önhurkos, sem több él nélküli gráfot egyszerű gráfnak nevezik.Több grafikon:Egy gráfot akkor mondunk Multi-nak, ha több élből áll, de önhurkok nélkül.Álgrafikon:Az önhurkos és több élű gráfot pszeudográfnak nevezzük.Nem irányított grafikon:A nem irányított élekből álló gráfot nem irányított gráfnak nevezzük.Irányított grafikon:A csúcsok közötti irányított élekből álló gráfot irányított gráfnak nevezzük.Összekapcsolt grafikon:Egy olyan gráfot, amelynek minden csúcspárja között legalább egyetlen útvonal van, összekapcsolt gráfnak nevezzük.Leválasztott grafikon:Az olyan gráfot, ahol legalább egy csúcspár között nincs út, szétkapcsolt gráfnak nevezzük.Normál grafikon:Azokat a gráfokat, amelyekben minden csúcsnak azonos a foka, reguláris gráfnak nevezzük.Teljes grafikon:Az olyan gráfot, amelyben minden csúcsnak van éle minden csúcspár között, teljes gráfnak nevezzük.Ciklusgrafikon:Egy gráfot ciklusnak nevezünk, ha legalább három csúcsa és éle van, amelyek ciklust alkotnak.Ciklikus grafikon:Egy gráfot akkor és csak akkor nevezünk ciklikusnak, ha legalább egy ciklus létezik.Aciklikus grafikon:A nulla ciklusú gráfot aciklikus gráfnak nevezzük.Véges gráf:A véges számú csúcsot és élt tartalmazó gráfot véges gráfnak nevezzük.Végtelen gráf:A végtelen számú csúcsot és élt tartalmazó gráfot végtelen gráfnak nevezzük.Kétrészes grafikon:Bipartite gráfnak nevezzük azt a gráfot, ahol a csúcsok független A és B halmazokra oszthatók, és az A halmaz összes csúcsát csak a B halmazban lévő csúcsokhoz kell kapcsolni néhány éllel.Síkdiagram:Egy gráfot síknak nevezünk, ha meg tudjuk rajzolni egyetlen síkban, ahol két él metszi egymást.Euler grafikon:Egy gráfot akkor és csak akkor mondunk Euler-nek, ha minden csúcsa páros fok.Hamiltoni grafikon:A Hamilton-körből álló összekapcsolt gráfot Hamilton-gráfnak nevezik.

A grafikonok néhány alkalmazása:

1. A grafikonok segítenek az útvonalak és hálózatok ábrázolásában a közlekedési, utazási és kommunikációs alkalmazásokban.
2. Grafikonok az útvonalak GPS-ben történő megjelenítésére szolgálnak.
3. A grafikonok abban is segítenek, hogy a közösségi hálózatokban és más hálózati alapú alkalmazásokban a kapcsolatokat ábrázoljuk.
4. A grafikonokat térképészeti alkalmazásokban használják.
5. A grafikonok felelősek a felhasználói preferenciák megjelenítéséért az e-kereskedelmi alkalmazásokban.
6. A grafikonokat a közüzemi hálózatokban is használják a helyi vagy önkormányzati vállalatok problémáinak azonosítására.
7. A grafikonok segítenek a szervezet erőforrásainak felhasználásának és elérhetőségének kezelésében is.
8. A grafikonokat a weboldalak dokumentumhivatkozási térképeinek elkészítésére is használják, hogy megjelenítsék az oldalak közötti kapcsolatot hiperhivatkozásokon keresztül.
9. A grafikonokat robotmozgásokban és neurális hálózatokban is használják.

Adatstruktúrák alapvető műveletei

A következő részben megvitatjuk azokat a különböző típusú műveleteket, amelyeket az adatok manipulálására végezhetünk minden adatszerkezetben:

Bejárás:Az adatstruktúra bejárása azt jelenti, hogy minden adatelemhez pontosan egyszer kell hozzáférni, így azok adminisztrálhatók. Például bejárásra van szükség az osztályon dolgozó összes alkalmazott nevének kinyomtatása közben.Keresés:A keresés egy másik adatszerkezeti művelet, amely egy vagy több olyan adatelem helyének megtalálását jelenti, amelyek megfelelnek bizonyos megszorításoknak. Ilyen adatelem az adott adatelem-készletben lehet, vagy nem. Például a keresési művelettel megkereshetjük az összes olyan munkatárs nevét, akik több mint 5 éves tapasztalattal rendelkeznek.Beillesztés:A beillesztés új adatelemek beszúrását vagy hozzáadását jelenti a gyűjteményhez. Használhatjuk például a beszúrási műveletet a vállalat által nemrég felvett új alkalmazott adatainak hozzáadásához.Törlés:A törlés egy adott adatelem eltávolítását vagy törlését jelenti az adatelemek adott listájából. Például a törlési művelettel törölhetjük a munkahelyét elhagyó alkalmazott nevét.Válogatás:A rendezés azt jelenti, hogy az adatelemeket az alkalmazás típusától függően növekvő vagy csökkenő sorrendbe rendezi. A rendezési művelettel például ábécé sorrendbe rendezhetjük egy osztályon az alkalmazottak nevét, vagy megbecsülhetjük a hónap legjobb három teljesítőjét úgy, hogy csökkenő sorrendbe rendezzük az alkalmazottak teljesítményét, és kivonjuk a három legjobb adatait.Összeolvad:Az összevonás azt jelenti, hogy két rendezett lista adatelemeit egyesítjük annak érdekében, hogy a rendezett adatelemek egyetlen listája legyen.Teremt:A Create művelet a program adatelemei számára memória lefoglalására szolgál. Ezt a műveletet deklarációs utasítással tudjuk végrehajtani. Az adatstruktúra létrehozása az alábbiak szerint történhet:
1. Fordítási idő
2. Futásidő
   Például a malloc() függvény a C nyelvben adatstruktúra létrehozására szolgál.
Kiválasztás:A kijelölés egy adott adat kiválasztását jelenti a rendelkezésre álló adatok közül. Bármilyen adatot kiválaszthatunk a cikluson belüli feltételek megadásával.Frissítés:A Frissítés művelet lehetővé teszi, hogy frissítsük vagy módosítsuk az adatstruktúrában lévő adatokat. Bármilyen adatot frissíthetünk a cikluson belüli feltételek megadásával, például a Kiválasztás művelettel.Hasítás:A Felosztás művelet lehetővé teszi, hogy az adatokat különböző alrészekre ossza fel, csökkentve a teljes folyamat befejezési idejét.

Az absztrakt adattípus megértése

Mint a National Institute of Standards and Technology (NIST) , az adatstruktúra információk elrendezése, általában a memóriában, a jobb algoritmus-hatékonyság érdekében. Az adatstruktúrák tartalmaznak csatolt listákat, veremeket, sorokat, fákat és szótárakat. Lehetnek elméleti entitások is, például egy személy neve és címe.

gépirat mindegyik

A fent említett definícióból arra a következtetésre juthatunk, hogy az adatszerkezetben a műveletek a következőket tartalmazzák:

1. Magas szintű absztrakciók, például egy elem hozzáadása vagy törlése a listáról.
2. Elemek keresése és rendezése a listában.
3. A lista legmagasabb prioritású elemének elérése.

Amikor az adatstruktúra ilyen műveleteket hajt végre, azt an Absztrakt adattípus (ADT) .

Meghatározhatjuk adatelemek halmazaként az adatokkal végzett műveletekkel együtt. Az „absztrakt” kifejezés arra utal, hogy az adatokat és a rajtuk definiált alapvető műveleteket a megvalósításuktól függetlenül tanulmányozzuk. Azt tartalmazza, hogy mit tehetünk az adatokkal, nem pedig azt, hogy hogyan.

Az ADI implementáció tárolóstruktúrát tartalmaz az alapvető műveletek adatelemeinek és algoritmusainak tárolására. Az összes adatstruktúra, például egy tömb, linkelt lista, sor, verem stb., az ADT példája.

Az ADT-k használatának előnyeinek megértése

A való világban a programok új megszorítások vagy követelmények következtében fejlődnek, így egy program módosítása általában egy vagy több adatstruktúra megváltoztatását igényli. Tegyük fel például, hogy egy új mezőt szeretnénk beszúrni egy alkalmazott nyilvántartásába, hogy nyomon követhessük az egyes alkalmazottak további részleteit. Ebben az esetben javíthatjuk a program hatékonyságát, ha egy tömböt cserélünk Linked szerkezetre. Ilyen helyzetben nem alkalmas minden olyan eljárás átírása, amely a módosított struktúrát használja. Ezért jobb alternatíva az, ha elválasztjuk az adatstruktúrát a megvalósítási információitól. Ez az elv az absztrakt adattípusok (ADT) használatában.

Az adatstruktúrák néhány alkalmazása

Íme néhány adatszerkezeti alkalmazás:

1. Az adatstruktúrák segítenek az adatok rendszerezésében a számítógép memóriájában.
2. Az adatstruktúrák az információk adatbázisokban való megjelenítését is segítik.
3. Az adatstruktúrák lehetővé teszik az adatok közötti kereséshez algoritmusok megvalósítását (például keresőmotor).
4. Használhatjuk az adatstruktúrákat az adatok manipulálására szolgáló algoritmusok megvalósítására (például szövegszerkesztők).
5. Az algoritmusokat adatszerkezetek (például adatbányászok) segítségével is megvalósíthatjuk adatok elemzésére.
6. Az adatstruktúrák támogatják az adatok generálására szolgáló algoritmusokat (például véletlenszám-generátort).
7. Az adatstruktúrák az adatok tömörítésére és kicsomagolására szolgáló algoritmusokat is támogatják (például egy zip segédprogram).
8. Az adatstruktúrákat is használhatjuk az adatok titkosítására és visszafejtésére szolgáló algoritmusok megvalósítására (például biztonsági rendszer).
9. A Data Structures segítségével olyan szoftvereket építhetünk, amelyek képesek fájlokat és könyvtárakat kezelni (Például egy fájlkezelő).
10. Olyan szoftvereket is fejleszthetünk, amelyek Data Structures segítségével grafikákat tudnak megjeleníteni. (Például egy webböngésző vagy egy 3D renderelő szoftver).

Azokon kívül, amint azt korábban említettük, az adatstruktúráknak számos más alkalmazása is segíthet nekünk bármilyen kívánt szoftver létrehozásában.