Ebben a cikkben a fa bejárását tárgyaljuk az adatstruktúrában. A „fa bejárása” kifejezés egy fa minden csomópontjának bejárását vagy meglátogatását jelenti. Egyetlen módja van a lineáris adatstruktúra bejárásának, például a csatolt lista, a sor és a verem. Míg a fán való áthaladásnak többféle módja van, amelyek az alábbiak szerint vannak felsorolva:
- Előrendelés bejárás
- Rendbejárás
- Postai utalvány bejárás
Tehát ebben a cikkben a fán való áthaladás fent felsorolt technikáit tárgyaljuk. Most kezdjük el megvitatni a fák bejárásának módjait.
Előrendelés bejárás
Ez a technika a „root left right” politikát követi. Ez azt jelenti, hogy először a gyökércsomópontot keresik fel, majd a bal oldali részfát rekurzívan, végül a jobb oldali részfát rekurzívan bejárják. Mivel a gyökércsomópont a bal és jobb részfa előtt (vagy elő) bejárásra kerül, ezt előrendelési bejárásnak nevezzük.
Tehát az előrendelési bejárás során minden csomópontot mindkét részfa előtt felkeresnek.
Az előrendelési bejárás alkalmazásai a következők:
- A fa másolatának létrehozására szolgál.
- Használható kifejezési fa előtag kifejezésének lekérésére is.
Algoritmus
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Példa
Most pedig lássuk az előrendelési bejárási technika példáját.
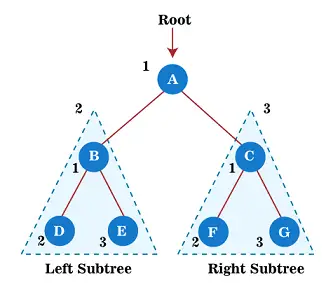
Most kezdje el alkalmazni az előrendelési bejárást a fenti fán. Először bejárjuk a gyökércsomópontot A; ezután lépjen a bal oldali részfájára B , amely előrendelésben is bejárható lesz.
Tehát a bal oldali B részfa esetében először a gyökércsomópont B átjárja magát; ezt követően a bal oldali részfa D bejárják. Node óta D nincs gyereke, lépjen a jobb oldali részfára ÉS . Mivel az E csomópontnak sincsenek gyermekei, az A gyökércsomópont bal oldali részfájának bejárása befejeződött.
a monitorom mérete
Most lépjen az A gyökércsomópont jobb oldali részfája felé, amely C. Tehát a jobb C részfához először a gyökércsomópontot C bejárta magát; ezt követően a bal oldali részfa F bejárják. Node óta F nincs gyereke, lépjen a jobb oldali részfára G . Mivel a G csomópontnak sincsenek gyermekei, az A gyökércsomópont jobb oldali részfájának bejárása befejeződött.
Ezért a fa összes csomópontját bejárjuk. Tehát a fenti fa előrendelési bejárásának eredménye:
A → B → D → E → C → F → G
Ha többet szeretne megtudni az előrendelési bejárásról az adatstruktúrában, kövesse a linket Előrendelés bejárás .
Postai utalvány bejárás
Ez a technika a „bal-jobb gyökér” politikát követi. Ez azt jelenti, hogy a gyökércsomópont első bal oldali részfája bejárásra kerül, ezt követően rekurzívan bejárja a jobb oldali részfát, végül pedig a gyökércsomópontot. Mivel a gyökércsomópontot a bal és a jobb részfa után (vagy utána) kell bejárni, ezt postorder bejárásnak nevezzük.
java math.random
Tehát egy utólagos bejárás során minden csomópontot mindkét részfa után keresünk fel.
Az utólagos bejárás alkalmazásai a következők:
- A fa törlésére szolgál.
- Használható kifejezési fa postfix kifejezésének lekérésére is.
Algoritmus
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Példa
Most pedig lássuk a postorder bejárás technikájának példáját.

Most kezdje el alkalmazni a postorder bejárást a fenti fán. Először bejárjuk a bal oldali B részfát, amelyet utólagos sorrendben fogunk bejárni. Ezt követően bejárjuk a megfelelő részfát C postorderben. És végül a fenti fa gyökércsomópontja, azaz A , áthaladva.
Tehát a B bal oldali részfa esetében először a bal oldali részfa D bejárják. Node óta D nincs gyereke, menjen át a megfelelő részfán ÉS . Mivel az E csomópontnak sincsenek gyermekei, lépjen a gyökércsomópontra B. Csomópont bejárása után B, az A gyökércsomópont bal oldali részfájának bejárása befejeződött.
Most menjen az A gyökércsomópont jobb részfája felé, amely C. Tehát a C jobb oldali részfához először a bal oldali részfája F bejárják. Node óta F nincs gyereke, menjen át a megfelelő részfán G . Mivel a G csomópontnak sincsenek gyermekei, ezért végül a jobb oldali részfa gyökércsomópontja, azaz C, bejárják. Az A gyökércsomópont jobb oldali részfájának bejárása befejeződött.
Végezetül menjen át egy adott fa gyökércsomópontján, azaz A . A gyökércsomópont bejárása után az adott fa utólagos bejárása befejeződik.
xml megjegyzés
Ezért a fa összes csomópontját bejárjuk. Tehát a fenti fa postorder bejárásának eredménye:
D → E → B → F → G → C → A
Ha többet szeretne megtudni a postorder bejárásáról az adatstruktúrában, kövesse a linket Postai utalvány bejárás .
Rendbejárás
Ez a technika a „bal gyökér jobb” irányelvet követi. Ez azt jelenti, hogy a gyökércsomópont bejárása után először a bal oldali részfát keresik fel, végül pedig a jobb oldali részfát. Mivel a gyökércsomópont a bal és a jobb részfa között van bejárva, ezt inorder bejárásnak nevezik.
Tehát az inorder bejárás során minden csomópontot a részfái között keresünk fel.
Az Inorder bejárás alkalmazásai a következők:
- A BST csomópontok növekvő sorrendben való megjelenítésére szolgál.
- Használható kifejezési fa előtag kifejezésének lekérésére is.
Algoritmus
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Példa
Most lássuk az Inorder bejárási technika példáját.
regressziós tesztelés a szoftvertesztben

Most kezdje el alkalmazni az inorder bejárást a fenti fán. Először áthaladunk a bal oldali részfán B hogy sorrendben lesz bejárva. Ezt követően bejárjuk a gyökércsomópontot A . És végül a megfelelő részfa C sorrendben halad át.
Tehát a bal oldali részfához B , először a bal oldali részfa D bejárják. Node óta D nincs gyereke, így bejárása után node B bejárjuk, és végül a B csomópont jobb oldali részfája, azaz ÉS , áthaladva. Az E csomópontnak szintén nincsenek gyermekei; ezért az A gyökércsomópont bal oldali részfájának bejárása befejeződött.
Ezt követően járjuk be egy adott fa gyökércsomópontját, azaz A .
Végül haladjunk az A gyökércsomópont jobb oldali részfája felé, amely C. Tehát a C jobb részfához; először a bal oldali részfája F bejárják. Node óta F nincs gyereke, node C bejárjuk, és végül a C csomópont jobb oldali részfája, azaz G , áthaladva. A G csomópontnak szintén nincsenek gyermekei; ezért az A gyökércsomópont jobb oldali részfájának bejárása befejeződött.
Mivel a fa összes csomópontját bejártuk, az adott fa sorrendben történő bejárása befejeződik. A fenti fa inorder bejárásának kimenete -
D → B → E → A → F → C → G
Ha többet szeretne megtudni az adatszerkezeti sorrend bejárásáról, kövesse a linket Inorder bejárás .
A fa bejárási technikák összetettsége
A fentebb tárgyalt fa bejárási technikák időbeli összetettsége az Tovább) , ahol 'n' akkora, mint egy bináris fa.
Míg a fentebb tárgyalt fa bejárási technikák térbonyolultsága az O(1) ha nem vesszük figyelembe a függvényhívások veremméretét. Ellenkező esetben ezeknek a technikáknak a térbeli összetettsége az O(h) , ahol 'h' a fa magassága.
jpa vs hibernate
Fa bejárás megvalósítása
Most pedig lássuk a fent tárgyalt technikák megvalósítását különböző programozási nyelvek használatával.
Program: Írjon programot a fa bejárási technikák megvalósítására C nyelven.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Kimenet

Program: Írjon programot a fa bejárási technikák C# nyelven való megvalósítására.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Kimenet

Program: Írjon programot a fa bejárási technikák megvalósítására C++ nyelven.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Kimenet
A fenti kód végrehajtása után a kimenet a következő lesz:

Következtetés
Ebben a cikkben a fa bejárásának különböző típusait tárgyaltuk: előrendelési bejárás, sorrendbejárás és utólagos bejárás. Láttuk ezeket a technikákat az algoritmusokkal, példákkal, összetettséggel és megvalósítással együtt C, C++, C# és java nyelven.
Szóval ennyi a cikkről. Remélhetőleg hasznos és informatív lesz számodra.
