Ebben a cikkben az adatszerkezetben az inorder bejárást tárgyaljuk.
Ha a csomópontokat növekvő sorrendben akarjuk bejárni, akkor az inorder bejárást használjuk. Az alábbi lépések szükségesek az inorder bejárásához:
- Látogassa meg a bal oldali részfa összes csomópontját
- Látogassa meg a gyökér csomópontot
- Látogassa meg a jobb oldali részfa összes csomópontját
A lineáris adatstruktúráknak, például a veremnek, a tömbnek, a sornak stb., csak egy módja van az adatok bejárására. De a hierarchikus adatstruktúrákban, mint pl fa, többféle mód van az adatok bejárására. Itt egy másik módot fogunk tárgyalni a fa adatszerkezetében, azaz az inorder bejárásról.
Az inorder bejáráshoz két megközelítést alkalmaznak:
- Rendelje meg a bejárást a Recursion használatával
- Rendbejárás iteratív módszerrel
Inorder bejárási technika követi a Bal gyökér Jobb irányelv. Itt a Left Root Right azt jelenti, hogy először a gyökércsomópont bal oldali részfáján, majd a gyökércsomóponton, majd a gyökércsomópont jobb oldali részfáján járunk be. Itt már maga a sorrend neve is azt sugallja, hogy a gyökércsomópont a bal és a jobb oldali részfa közé kerül.
string cserélje ki az összes Java-t
Az inorder bejárást rekurzív és iteratív technikák segítségével is tárgyaljuk. Kezdjük először az inorder bejárással rekurzió segítségével.
Inorder bejárás rekurzió segítségével
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Példa az inorder bejárásra
Most lássunk egy példát az inorder bejárásra. Egy példa segítségével könnyebb lesz megérteni az inorder bejárás eljárását.
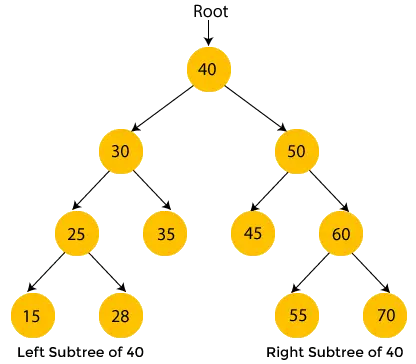
A sárga színű csomópontok még nincsenek felkeresve. Most a fenti fa csomópontjain fogjuk bejárni az inorder bejárást.
- Itt a 40 a gyökércsomópont. A 40-es bal oldali részfájára lépünk, azaz 30-ra, és annak is van 25-ös részfája, tehát ismét a 25-ös bal oldali részfájára lépünk, ami 15. Itt a 15-nek nincs részfája, tehát nyomtatás 15 és lépjen a szülőcsomópontja felé, a 25.
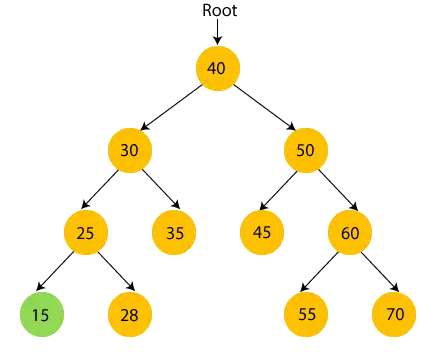
- Most, nyomtatás 25 és lépjen a 25-ös jobb oldali részfára.
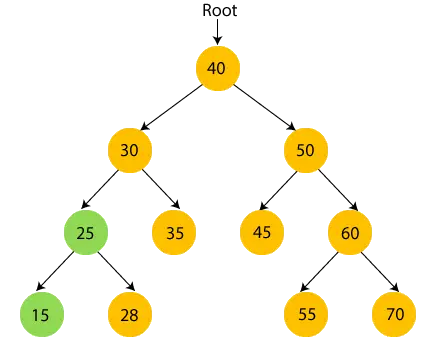
- Most, nyomtatás 28 és lépjen a 25 gyökércsomópontjára, ami a 30.
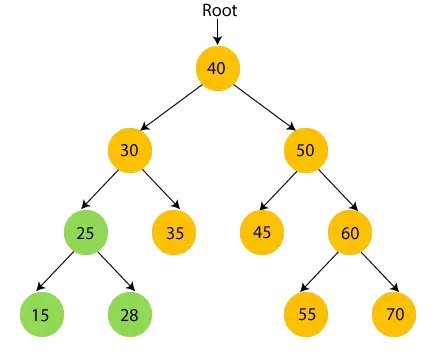
- Tehát a 30-as bal oldali részfa meglátogatva. Most, nyomtatás 30 és költözz a 30 éves jobb gyerekhez.
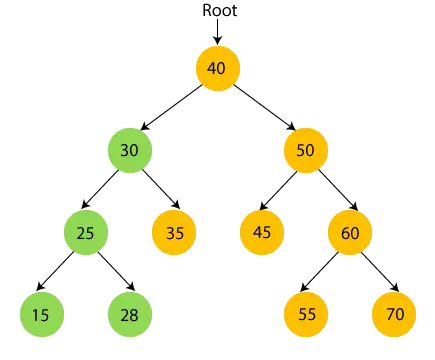
- Most, nyomtatás 35 és lépjen a 30 gyökércsomópontjára.
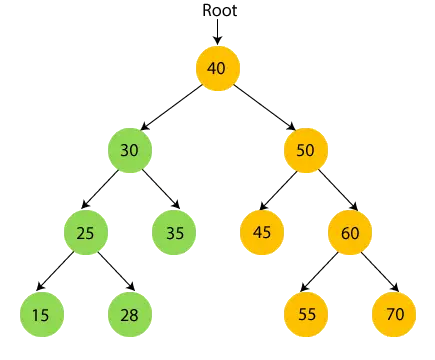
- Most, gyökércsomópont nyomtatása 40 és lépjen a jobb oldali részfájára.
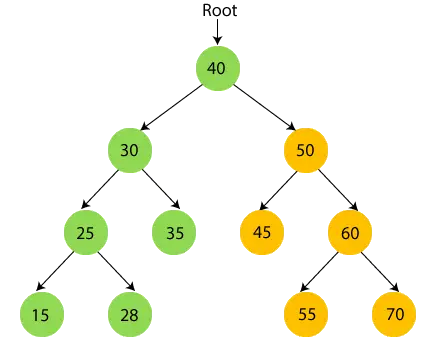
- Most rekurzívan menjen át a 40 jobb oldali részfáján, amely 50.
50-nek van részfája, tehát először menjen át az 50-es bal oldali részfán, amely 45. 45-nek nincs gyereke, tehát nyomtatás 45 és lépjen a gyökércsomópontjára.
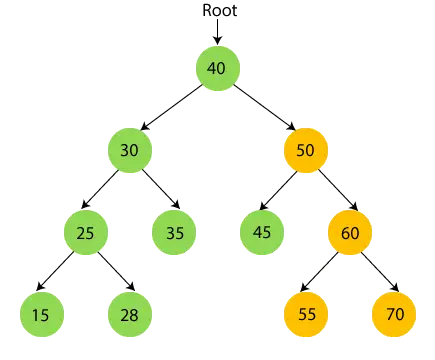
- Most nyomtatás 50 és lépjen az 50-es jobb oldali részfára, amely 60.
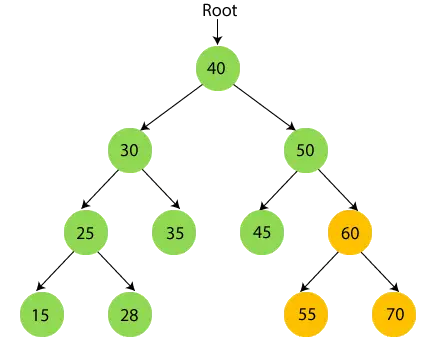
- Most rekurzívan járja be az 50-es jobb oldali részfát, ami 60. A 60-nak van részfája, tehát először a 60-as bal oldali részfán, amely 55. Az 55-nek nincs gyermeke, tehát nyomtatás 55 és lépjen a gyökércsomópontjára.
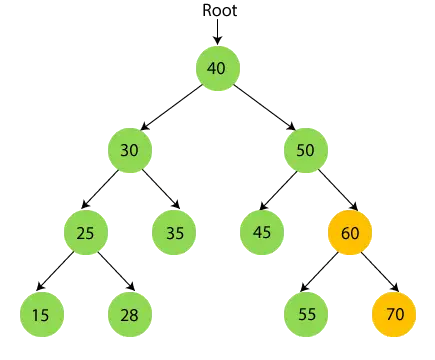
- Most nyomtatás 60 és lépjen a 60 jobb oldali részfájára, ami 70.
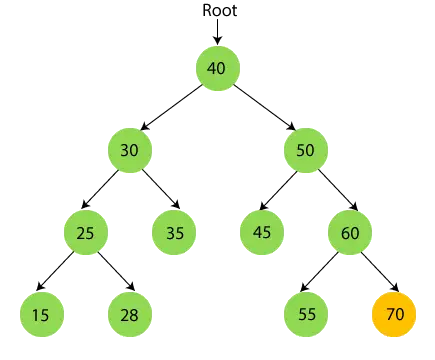
- Most nyomtatás 70.
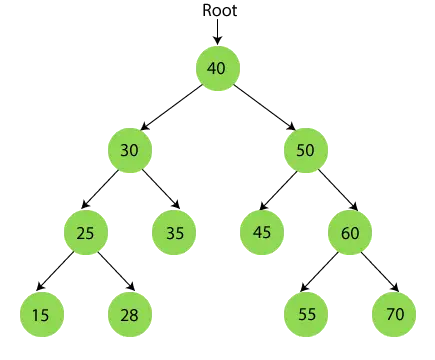
Az inorder bejárás befejezése után a végső kimenet:
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Az Inorder bejárásának összetettsége
Az Inorder bejárás időbeli összetettsége az Tovább), ahol 'n' a bináris fa mérete.
Ezzel szemben az inorder bejárás térbeli összetettsége az O(1), ha nem vesszük figyelembe a függvényhívások veremméretét. Ellenkező esetben az inorder bejárás térbonyolultsága az O(h), ahol 'h' a fa magassága.
előrendelési bejárás
Inorder bejárás megvalósítása
Most pedig lássuk az inorder bejárás megvalósítását különböző programozási nyelveken.
Program: Írjon programot az inorder bejárás megvalósítására C nyelven.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Kimenet
jgombot

Program: Írjon programot az inorder bejárás megvalósítására C++ nyelven.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Kimenet

Program: Írjon programot az inorder bejárás megvalósítására Java nyelven.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Kimenet

Szóval ennyi a cikkről. Reméljük, hogy a cikk hasznos és informatív lesz az Ön számára.











