Ebben a cikkben az előrendelési bejárást tárgyaljuk az adatstruktúrában. A lineáris adatstruktúráknak, például a veremnek, a tömbnek, a sornak stb., csak egy módja van az adatok bejárására. De egy hierarchikus adatszerkezetben, mint pl fa , többféle módon lehet bejárni az adatokat.
Az előrendelési bejárás során először a gyökércsomópont, majd a bal oldali részfa, ezt követően pedig a jobb oldali részfa. Az előrendelési bejárás folyamata a következőképpen ábrázolható:
root → left → right
A gyökércsomópont mindig először jár be az előrendelési bejárás során, míg az utólagos bejárás utolsó eleme. Az előrendelési bejárás egy fa előtag kifejezésének lekérésére szolgál.
Az előrendelési bejárás végrehajtásának lépései a következők:
hogyan lehet egy karakterláncot intté alakítani
- Először keresse fel a gyökér csomópontot.
- Ezután keresse fel a bal oldali részfát.
- Végül keresse fel a megfelelő részfát.
Az előrendelési bejárási technika követi a Gyökér Bal Jobb irányelv. Maga az előrendelés név azt sugallja, hogy először a gyökércsomópontot kell bejárni.
Algoritmus
Most pedig lássuk az előrendelési bejárás algoritmusát.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: Write TREE -> DATA Step 3: PREORDER(TREE -> LEFT) Step 4: PREORDER(TREE -> RIGHT) [END OF LOOP] Step 5: END
Példa az előrendelési bejárásra
Most pedig lássunk egy példát az előrendelési bejárásra. Egy példa segítségével könnyebb lesz megérteni az előrendelési bejárás folyamatát.
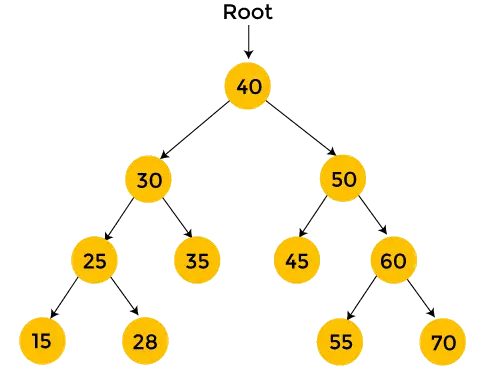
A sárga színű csomópontok még nincsenek felkeresve. Most a fenti fa csomópontjain fogunk bejárni az előrendelési bejárás segítségével.
- Kezdje a 40-es gyökércsomóponttal. Először is, nyomtatás 40 majd rekurzívan bejárjuk a bal oldali részfát.
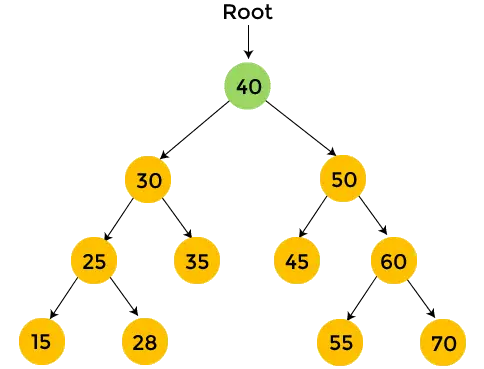
- Most lépjen a bal oldali részfára. A bal oldali részfa gyökércsomópontja 30. Nyomtatás 30 , és lépjen a 30-as bal oldali részfa felé.
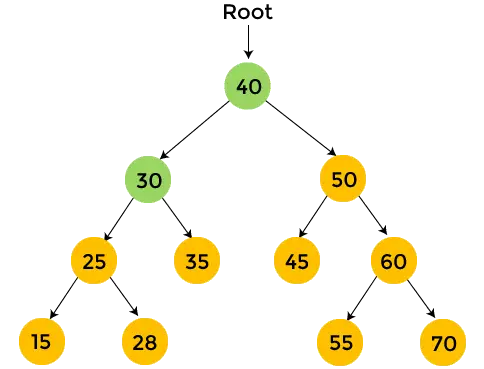
- A 30-as bal részfában van egy 25-ös elem, tehát nyomtatás 25 , és menjen át a 25 bal oldali részfáján.
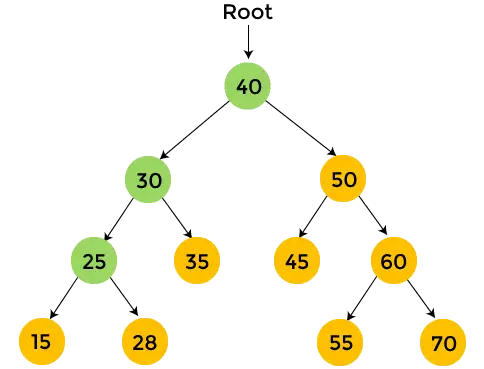
- A 25-ös bal részfában van egy 15-ös elem, a 15-ösnek pedig nincs részfája. Így, nyomtatás 15 , és lépjen a 25-ös jobb oldali részfára.
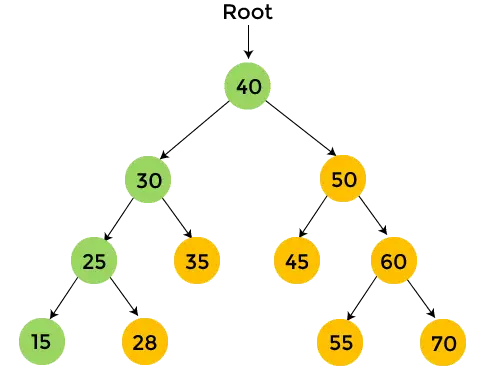
- A 25 jobb oldali részfájában 28 található, a 28-ban pedig nincs részfa. Így, nyomtatás 28 , és lépjen a 30-as jobb oldali részfára.
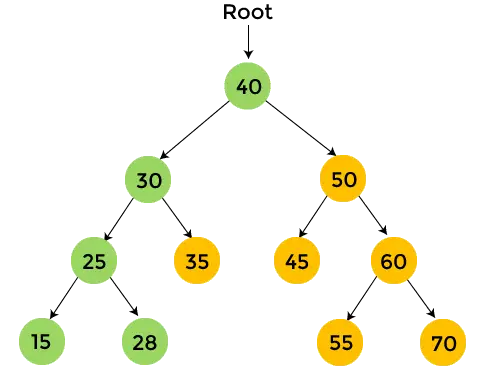
- A 30 jobb oldali részfájában van 35, amelynek nincs részfája. Így nyomtatás 35 , és menjen át a 40-es jobb oldali részfán.
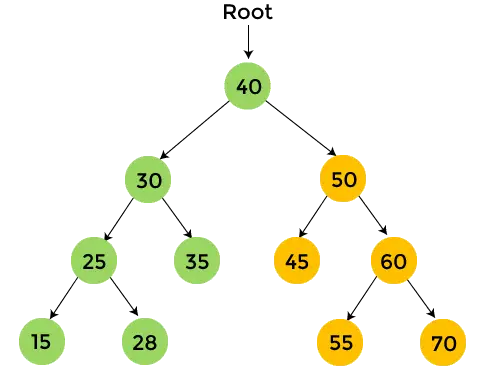
- A 40 jobb oldali részfájában 50 található. Nyomtatás 50 , és menjen át az 50-es bal oldali részfán.
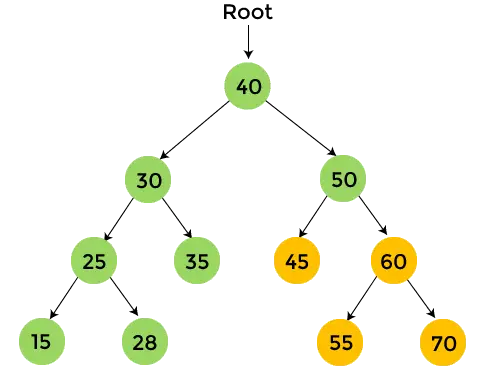
- Az 50-es bal oldali részfában 45 van, amelynek nincs gyermeke. Így, nyomtatás 45 , és menjen át az 50-es jobb oldali részfán.
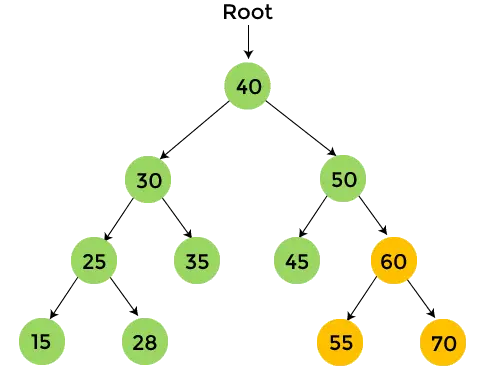
- Az 50 jobb oldali részfájában 60 található. Nyomtatás 60 és menjen át a 60-as bal oldali részfán.
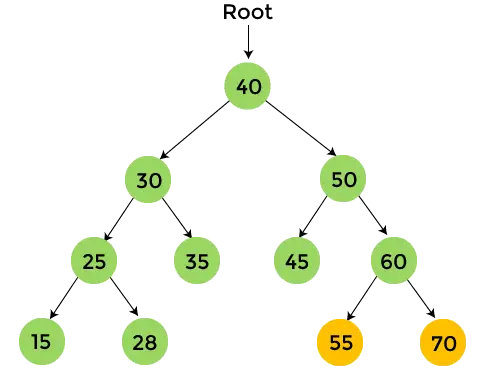
- A 60-as bal részfában 55 van, amelynek nincs gyermeke. Így, nyomtatás 55 és lépjen a 60-as jobb oldali részfára.
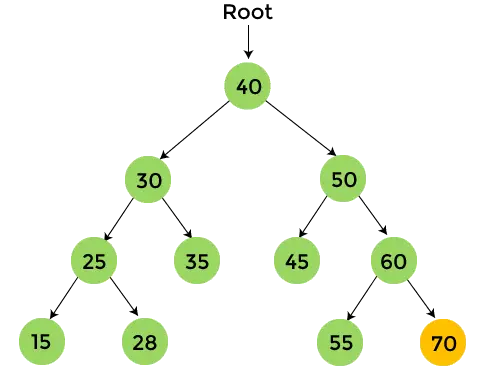
- A 60 jobb oldali részfájában 70 van, amelynek nincs gyermeke. Így, nyomtatás 70 és állítsa le a folyamatot.
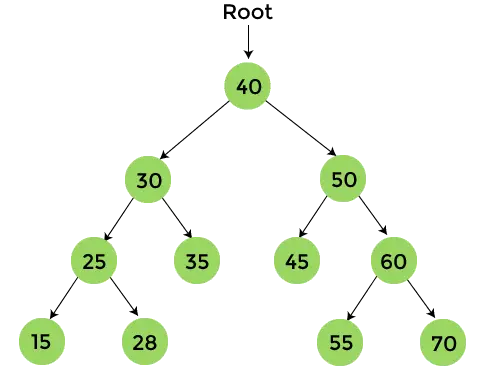
Az előrendelési bejárás befejezése után a végső kimenet:
40, 30, 25, 15, 28, 35, 50, 45, 60, 55, 70
Az előrendelési bejárás összetettsége
Az előrendelési bejárás időbeli összetettsége az Tovább) , ahol az 'n' a bináris fa mérete.
Ezzel szemben az előrendelési bejárás térbeli összetettsége az O(1) , ha nem vesszük figyelembe a függvényhívások veremméretét. Ellenkező esetben az előrendelési bejárás térbonyolultsága az O(h) , ahol a „h” a fa magassága.
különben ha java
Előrendelési bejárás megvalósítása
Most pedig lássuk az előrendelési bejárás megvalósítását különböző programozási nyelveken.
Program: Írjon programot az előrendelési bejárás megvalósítására C nyelven.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); return 0; } Kimenet
A fenti kód végrehajtása után a kimenet a következő lesz:

Program: Írjon programot az előrendelési bejárás megvalósítására C++ nyelven.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } int main() { struct node* root = createNode(39); root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-14.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(38); bt.root.left = new Node(28); bt.root.right = new Node(48); bt.root.left.left = new Node(23); bt.root.left.right = new Node(33); bt.root.left.left.left = new Node(13); bt.root.left.left.right = new Node(26); bt.root.right.left = new Node(43); bt.root.right.right = new Node(58); bt.root.right.right.left = new Node(53); bt.root.right.right.right = new Node(68); Console.WriteLine('Preorder traversal of given binary tree is - '); bt.traversePreorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-15.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-16.webp" alt="Preorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Kimenet
A fenti kód végrehajtása után a kimenet a következő lesz:

Program: Írjon programot az előrendelési bejárás megvalósítására Java nyelven.
matematikai módszerek java-ban
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } Kimenet
A fenti kód végrehajtása után a kimenet a következő lesz:

Szóval ennyi a cikkről. Reméljük, hogy a cikk hasznos és informatív lesz az Ön számára.











