A konvolúciót sok mindenre használják, mint például deriváltak kiszámítására, élek észlelésére, elmosódások alkalmazására stb., és mindezt egy „konvolúciós kernel” segítségével végzik. A konvolúciós kernel egy nagyon kicsi mátrix, és ebben a mátrixban minden cellának van egy száma és egy rögzítési pontja is.
A rögzítési pontot arra használjuk, hogy ismerjük a rendszermag helyzetét a képhez képest. A kép bal felső sarkától kezdődik, és az egyes pixeleken egymás után mozog. A kernel a kép minden pozíciójában néhány pixel átfedésben van. Minden átfedésben lévő pixelt megszoroz, majd hozzáad. És az összeg az aktuális pozíció értékeként van beállítva.
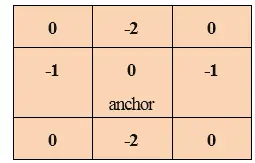
A konvolúció az a folyamat, amelyben a kép minden elemét hozzáadják a helyi szomszédokhoz, majd a kernel súlyozza azokat. Ez a matematikai konvolúció egyik formájához kapcsolódik.
A konvolúcióban a mátrix nem hajtja végre a hagyományos mátrixszorzást, hanem *-gal van jelölve.
Tegyük fel, hogy van két 3x3-as mátrix, az egyik kernel, a másik pedig egy képdarab. A konvolúció során a kernel sorait és oszlopait átfordítják, majd megszorozzák, majd összegzést hajtanak végre. Azok az elemek, amelyek a mátrix közepén, azaz a kép [2,2] részében vannak, a képmátrix súlyozott kombinációja lesz, és a súlyokat a kernel adja meg. Hasonlóképpen, a mátrix összes többi eleme súlyozásra kerül, majd a súlyok kiszámításra kerülnek.
A következő pszeudokód a konvolúciós folyamat leírására szolgál:
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
A konvolúció kiszámítható többszörös for ciklus használatával. A for ciklusok használata azonban sok ismételt számítást okoz, és a kép és a kernel mérete is megnő. A Discrete Fourier Transform technikával a konvolúció kiszámítása gyorsan elvégezhető. Ennél a technikánál a teljes konvolúciós műveletet egyszerű szorzássá alakítják.
A konvolúció során a probléma akkor jelentkezik, ha a kernel a széléhez vagy a sarkokhoz közel van, mivel a kernel kétdimenziós.
Ezeknek a problémáknak a leküzdése érdekében a következőket lehet tenni:
- Az egyiket figyelmen kívül lehet hagyni
- A szélek közelében további képpontok hozhatók létre.
További képpontok a következő módokon hozhatók létre:
- Az élpixel megkettőzése.
- Tükrözik a széleket
- A pixelek a másik végéről másolhatók.
