A gépi tanulás a mesterséges intelligencia egyik ága, amely lehetővé teszi a gépek számára, hogy adatelemzést végezzenek és előrejelzéseket készítsenek. Ha azonban a gépi tanulási modell nem pontos, akkor előrejelzési hibákat követhet el, és ezeket az előrejelzési hibákat általában torzításnak és eltérésnek nevezik. A gépi tanulásban ezek a hibák mindig jelen lesznek, mivel mindig van egy kis különbség a modell előrejelzései és a tényleges előrejelzések között. Az ML/adattudomány elemzőinek fő célja ezen hibák csökkentése a pontosabb eredmények elérése érdekében. Ebben a témában az elfogultságról és szórásról, a torzítás-variancia kompromisszumról, az alul- és túlillesztésről lesz szó. De mielőtt elkezdené, először értsük meg, mik a gépi tanulás hibái?
Hibák a gépi tanulásban?
A gépi tanulásban a hiba annak mértéke, hogy egy algoritmus milyen pontosan képes előrejelzéseket készíteni a korábban ismeretlen adatkészletre. E hibák alapján kiválasztják azt a gépi tanulási modellt, amely a legjobban teljesít az adott adatkészleten. A gépi tanulásban alapvetően kétféle hiba van, amelyek a következők:

függetlenül attól, hogy melyik algoritmust használtuk. Ezeknek a hibáknak az oka ismeretlen változók, amelyek értéke nem csökkenthető.
Mi az a Bias?
Általában a gépi tanulási modell elemzi az adatokat, mintákat keres bennük, és előrejelzéseket készít. A képzés során a modell megtanulja ezeket a mintákat az adatkészletben, és alkalmazza őket az előrejelzési tesztadatokhoz. Előrejelzések készítésekor különbség lép fel a modell által készített előrejelzési értékek és a tényleges értékek/várt értékek között , és ezt a különbséget torzítási hibáknak vagy elfogultságból eredő hibáknak nevezik . Úgy definiálható, hogy a gépi tanulási algoritmusok, például a lineáris regresszió nem képesek rögzíteni az adatpontok közötti valódi kapcsolatot. Minden algoritmus bizonyos mértékű torzítással kezdődik, mivel a torzítás a modell feltételezéseiből származik, ami megkönnyíti a célfüggvény megtanulását. Egy modell rendelkezik a következőkkel:
rendező Karan Johar
Általában a lineáris algoritmusok nagy torzítással rendelkeznek, mivel gyorsan tanulnak. Minél egyszerűbb az algoritmus, annál nagyobb a torzítás valószínűsége. Míg a nemlineáris algoritmusok gyakran alacsony torzítással rendelkeznek.
Néhány példa alacsony torzítású gépi tanulási algoritmusokra döntési fák, k-legközelebbi szomszédok és támogató vektorgépek . Ugyanakkor egy nagy torzítású algoritmus az Lineáris regresszió, lineáris diszkriminancia analízis és logisztikai regresszió.
A nagy torzítás csökkentésének módjai:
A nagy torzítás főként egy sokkal egyszerűbb modell miatt következik be. Az alábbiakban bemutatunk néhány módszert a nagy torzítás csökkentésére:
- Növelje a bemeneti jellemzőket, mivel a modell alul van beszerelve.
- Csökkentse a rendszerezési időtartamot.
- Használjon összetettebb modelleket, például tartalmazzon néhány polinomiális jellemzőt.
Mi az a varianciahiba?
A variancia meghatározza az előrejelzés variációjának mértékét, ha a különböző képzési adatokat használjuk. Egyszerű szavakkal, A variancia azt mutatja meg, hogy egy valószínűségi változó mennyiben tér el a várható értékétől. Ideális esetben egy modellnek nem szabad túlságosan változnia az egyik tanítási adatkészletről a másikra, ami azt jelenti, hogy az algoritmusnak jónak kell lennie a bemeneti és kimeneti változók közötti rejtett leképezés megértésében. Az eltérési hibák bármelyike alacsony szórás vagy nagy szórás.
öröklődés c++-ban
Alacsony szórás azt jelenti, hogy a betanítási adatkészlet változásaival a célfüggvény előrejelzése kismértékű eltérést mutat. Ugyanabban az időben, Magas szórás nagy eltéréseket mutat a célfüggvény előrejelzésében a betanítási adatkészlet változásaival.
A nagy varianciát mutató modell sokat tanul és jól teljesít a betanítási adatkészlettel, és nem általánosít jól a nem látott adatkészlettel. Ennek eredményeként egy ilyen modell jó eredményeket ad a betanítási adatkészlettel, de magas hibaarányt mutat a tesztadatkészletben.
Mivel nagy szórás mellett a modell túl sokat tanul az adatkészletből, ez a modell túlillesztéséhez vezet. A nagy szórású modellek a következő problémákkal küzdenek:
- A nagy szórású modell túlillesztéshez vezet.
- Növelje a modell bonyolultságát.
Általában a nemlineáris algoritmusok nagy rugalmassággal rendelkeznek, hogy illeszkedjenek a modellhez, nagy a varianciájuk.

Néhány példa az alacsony szórású gépi tanulási algoritmusokra: Lineáris regresszió, logisztikai regresszió és lineáris diszkriminancia analízis . Ugyanakkor a nagy szórású algoritmusok igen döntési fa, Support Vector Machine és K-legközelebbi szomszédok.
c karakterláncok tömbje
A nagy szórás csökkentésének módjai:
- Csökkentse a bemeneti jellemzőket vagy a paraméterek számát, ha a modell túl van szerelve.
- Ne használjon túl bonyolult modellt.
- Növelje az edzési adatokat.
- Növelje a rendszerezési időtartamot.
A torzítás-varianciák különböző kombinációi
A torzításoknak és eltéréseknek négy lehetséges kombinációja van, amelyeket az alábbi diagram szemléltet:

Az alacsony torzítás és az alacsony szórás kombinációja ideális gépi tanulási modellt mutat. Ez azonban gyakorlatilag nem lehetséges.
Magas torzítás és nagy szórás esetén az előrejelzések következetlenek és átlagosan pontatlanok is.
Hogyan lehet azonosítani a nagy szórást vagy a nagy torzítást?
Nagy variancia azonosítható, ha a modell rendelkezik:

- Alacsony edzési hiba és magas teszthiba.
A nagy torzítás azonosítható, ha a modell rendelkezik:
- Magas edzési hiba és a teszthiba szinte hasonló a képzési hibához.
Bias-Variance kompromisszum
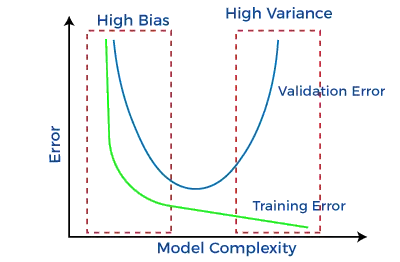
A gépi tanulási modell felépítése során nagyon fontos ügyelni a torzításra és a szórásra, hogy elkerüljük a túl- és alulillesztést a modellben. Ha a modell nagyon egyszerű, kevesebb paraméterrel, akkor alacsony szórású és nagy torzítású lehet. Míg ha a modell nagyszámú paraméterrel rendelkezik, akkor nagy variancia és alacsony torzítás lesz. Tehát egyensúlyt kell teremteni a torzítási és varianciahibák között, és ezt az egyensúlyt a torzítási hiba és a varianciahiba között úgy ismerjük a Bias-Variance kompromisszum.

A modell pontos előrejelzéséhez az algoritmusoknak alacsony szórásra és alacsony torzításra van szükségük. De ez nem lehetséges, mert a torzítás és a szórás összefügg egymással:
- Ha csökkentjük a szórást, az növeli a torzítást.
- Ha csökkentjük a torzítást, az növeli a szórást.
A torzítás-variáns kompromisszum központi kérdés a felügyelt tanulásban. Ideális esetben olyan modellre van szükségünk, amely pontosan rögzíti a tanítási adatok szabályszerűségeit, és egyidejűleg jól általánosít a nem látott adatkészlettel. Sajnos ez nem lehetséges egyszerre. Mert egy nagy szórású algoritmus jól teljesíthet a betanítási adatokkal, de túlillesztéshez vezethet a zajos adatokhoz. Míg a nagy torzítású algoritmus egy sokkal egyszerűbb modellt hoz létre, amely talán nem is rögzíti az adatok fontos szabályszerűségeit. Tehát meg kell találnunk egy édes pontot a torzítás és a szórás között, hogy optimális modellt hozzunk létre.
Ezért a A Bias-Variance kompromisszum arról szól, hogy megtaláljuk a megfelelő helyet az elfogultság és az eltérési hibák közötti egyensúly megteremtéséhez.
