Megértés előtt B fa és B+ fa különbségeket, külön kell ismernünk a B fát és a B+ fát.
Mi az a B fa?
B fa egy önkiegyensúlyozó fa, és ez egy m-irányú fa, ahol m határozza meg a fa sorrendjét. Btree általánosítása a Bináris keresőfa amelyben egy csomópontnak egynél több kulcsa és kettőnél több gyermeke lehet az értékétől függően m . A B fában az adatok rendezési sorrendben vannak megadva, a bal oldali részfában alacsonyabb értékek, a jobb oldali részfák pedig magasabbak.
string tömb létrehozása java-ban
A B fa tulajdonságai
A B fa tulajdonságai a következők:
- A B fában az összes levélcsomópontnak azonos szinten kell lennie, míg egy bináris fa esetében a levélcsomópontok különböző szinteken lehetnek.
Értsük meg ezt a tulajdonságot egy példán keresztül.
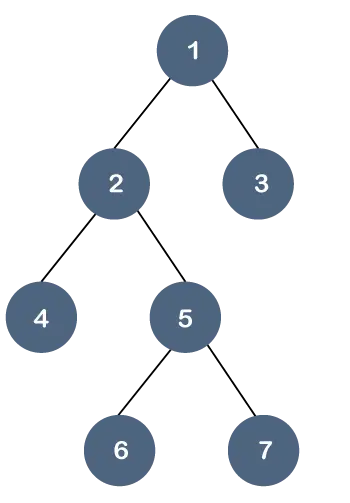
A fenti fában az összes levélcsomópont nem azonos szinten van, de két gyermekük van. Ezért azt mondhatjuk, hogy a fenti fa a bináris fa de nem B fa.
- Ha a Bfa m-es sorrendű, akkor minden csomópontnak maximuma lehet m Minimális gyermekek esetén a levélcsomópontok nulla, a gyökércsomópont két gyermek, a belső csomópontok felső határa m/2.
- Minden csomópontnak maximum (m-1) kulcsa lehet. Például, ha m értéke 5, akkor a kulcsok maximális értéke 4.
- A gyökércsomópontnak legalább egy kulcsa van, míg a gyökércsomópont kivételével az összes többi csomópontnak (a felső határa m/2 mínusz - 1) minimális kulcsa van.
- Ha a B fában végzünk beszúrást, akkor a csomópont mindig a levélcsomópontba kerül be.
Tegyük fel, hogy egy 3-as rendű B fát szeretnénk létrehozni 1-től 10-ig terjedő értékek beszúrásával.
1. lépés: Először is létrehozunk egy csomópontot 1 értékkel az alábbiak szerint:

2. lépés: A következő elem a 2, amely az 1 után következik, az alábbiak szerint:

3. lépés: A következő elem a 3, és a 2 után kerül beillesztésre az alábbiak szerint:

Mivel tudjuk, hogy minden csomópontnak maximum 2 kulcsa lehet, ezért ezt a csomópontot a középső elemen keresztül osztjuk fel. A középső elem 2, tehát átkerül a szülőjére. A 2-es csomópontnak nincs szülője, ezért ez lesz a gyökércsomópont az alábbiak szerint:

4. lépés: A következő elem a 4. Mivel a 4 nagyobb, mint 2 és 3, ezért a 3 után kerül hozzáadásra az alábbiak szerint:

5. lépés: A következő elem az 5. Mivel az 5 nagyobb, mint 2, 3 és 4, ezért a 4 után hozzáadódik az alábbiak szerint:

Mivel tudjuk, hogy minden csomópontnak maximum 2 kulcsa lehet, ezért ezt a csomópontot a középső elemen keresztül osztjuk fel. A középső elem 4, tehát a szülőjére kerül. A szülő a 2. csomópont; ezért a 2 után 4 lesz hozzáadva, az alábbiak szerint:

6. lépés: A következő elem a 6. Mivel a 6 nagyobb 2-nél, 4-nél és 5-nél, így a 6 az 5 után következik, amint az alább látható:

7. lépés: A következő elem a 7. Mivel a 7 nagyobb, mint 2, 4, 5 és 6, így a 7 a 6 után következik, ahogy az alábbiakban látható:

Mivel tudjuk, hogy minden csomópontnak maximum 2 kulcsa lehet, ezért ezt a csomópontot a középső elemen keresztül osztjuk fel. A középső elem 6, tehát a szülőjére kerül az alábbiak szerint:

De a 6-ot nem lehet hozzáadni 4 után, mert a csomópontnak maximum 2 kulcsa lehet, ezért ezt a csomópontot a középső elemen keresztül osztjuk fel. A középső elem 4, tehát a szülőjére kerül. Mivel a 4-es csomópontnak nincs szülője, a 4-es csomópont gyökércsomóponttá válik az alábbiak szerint:

Mi az a B+ fa?
A B+ fa fejlett önkiegyensúlyozott faként is ismert, mivel a fa gyökerétől a fa leveléig minden út azonos hosszúságú. Itt az azonos hosszúság azt jelenti, hogy az összes levélcsomópont ugyanazon a szinten található. Nem fog előfordulni, hogy a levél csomópontok egy része a harmadik, néhány pedig a második szinten fordul elő.
A B+ fa indexet többszintű indexnek tekintjük, de a B+ fa szerkezete nem hasonlít a többszintű index szekvenciális fájlokhoz.
Miért használják a B+ fát?
A B+ fa a rekordok nagyon hatékony tárolására szolgál azáltal, hogy a rekordokat indexelt módon tárolja a B+ fa indexelt struktúrájával. A többszintű indexelésnek köszönhetően gyorsabbá és egyszerűbbé válik az adatok elérése.
B+ fa csomóponti struktúra
A B+ fa csomóponti szerkezete mutatókat és kulcsértékeket tartalmaz, amelyek az alábbi ábrán láthatók:

Amint azt a fenti B+ fa csomóponti struktúrában láthatjuk, n-1 kulcsértéket tartalmaz (k1hogy kn-1) és n mutató (o1pn).
A csomópontban elhelyezett keresési kulcsértékek rendezett sorrendben kerülnek tárolásra. Így, ha i
A különböző típusú csomópontok korlátozása
Legyen 'b' a B+ fa sorrendje.
Nem levél csomópont
escape karakter java
Legyen 'm' egy csomópont gyermekeinek száma, akkor a fa sorrendje és a gyermekek száma közötti összefüggés a következőképpen ábrázolható:

Legyen k a keresési kulcs értékei. A fa sorrendje és a keresési kulcs közötti kapcsolat a következőképpen ábrázolható:
Mivel tudjuk, hogy a mutatók száma megegyezik a keresőkulcs értékeivel plusz 1-gyel, így matematikailag a következőképpen írható fel:
Mutatók (vagy gyermekek) száma = keresőbillentyűk száma + 1
Ezért a mutatók maximális száma 'b' lenne, a mutatók minimális száma pedig a b/2 plafonfüggvénye.
Levélcsomópont
A levélcsomópont olyan csomópont, amely a B+ fa utolsó szintjén található, és minden levélcsomópont csak egy mutatót használ az egymáshoz való kapcsolódáshoz, hogy biztosítsa a szekvenciális hozzáférést a levél szintjén.
A levél csomópontjában a gyermekek maximális száma:

A keresőbillentyűk maximális száma:

Root Node
A gyerekek maximális száma a gyökércsomópont esetén: b
A minimális gyermeklétszám: 2
Speciális esetek a B+ fában
1. eset: Ha a gyökércsomópont az egyetlen csomópont a fában. Ebben az esetben a gyökércsomópont levélcsomóponttá válik.
Ebben az esetben a gyerekek maximális száma 1, azaz maga a gyökércsomópont, míg a gyerekek minimális száma b-1, ami megegyezik egy levélcsomópontéval.
Levélcsomópont ábrázolása B+ fában

A fenti ábrán a '.' a mutatót jelenti, míg a 10, 20 és 30 a kulcsértékek. A mutató tartalmazza azt a címet, amelyen a kulcsérték tárolva van, amint az a fenti ábrán látható.
Példa a B+ fára

A fenti ábrán a csomópont három kulcsértéket tartalmaz, azaz 9-et, 16-ot és 25-öt. A 9 előtt megjelenő mutató a 9-nél kisebb kulcsértékeket tartalmazza, amelyeket k képvisel.én. A 16 előtt megjelenő mutató a 9-nél nagyobb vagy egyenlő, de 16-nál kisebb kulcsértékeket tartalmazza, amelyeket kj képvisel. A 25 előtt megjelenő mutató tartalmazza a 16-nál nagyobb vagy egyenlő, de 25-nél kisebb kulcsértékeket, amelyeket k képviseln.
A B fa és a B+ fa közötti különbségek

A következő különbségek vannak a B fa és a B+ fa között:
| B fa | B+ fa |
|---|---|
| A B fában az összes kulcs és rekord mind a belső, mind a levélcsomópontokban tárolva van. | A B+ fában a kulcsok a belső csomópontokban tárolt indexek, a rekordok pedig a levélcsomópontokban tárolódnak. |
| A B fában a kulcsok nem tárolhatók ismételten, ami azt jelenti, hogy a kulcsok vagy rekordok nem duplikálódnak. | A B+ fában előfordulhat redundancia a kulcsok előfordulásában. Ebben az esetben a rekordok a levél csomópontokban, míg a kulcsok a belső csomópontokban tárolódnak, így redundáns kulcsok lehetnek jelen a belső csomópontokban. |
| A Btree-ben a levél csomópontjai nem kapcsolódnak egymáshoz. | A B+ fában a levél csomópontjai egymáshoz vannak kapcsolva, hogy biztosítsák a szekvenciális hozzáférést. |
| A Btree-ben a keresés nem túl hatékony, mert a rekordokat vagy levélben, vagy belső csomópontokban tárolják. | A B+ fában a keresés nagyon hatékony vagy gyorsabb, mivel az összes rekord a levél csomópontjaiban van tárolva. |
| A belső csomópontok törlése nagyon lassú és időigényes folyamat, mivel figyelembe kell vennünk a törölt kulcs gyermekét is. | A B+ fában a törlés nagyon gyors, mert minden rekord a levél csomópontjaiban van tárolva, így nem kell figyelembe vennünk a csomópont gyermekét. |
| A Btree-ben a szekvenciális hozzáférés nem lehetséges. | A B+ fában az összes levélcsomópont egy pointeren keresztül kapcsolódik egymáshoz, így lehetséges a szekvenciális hozzáférés. |
| A Btree-ben minél több hasítási műveletet hajtanak végre, amelyek miatt a magasság nő a szélességhez képest, | A B+ fának nagyobb a szélessége a magassághoz képest. |
| A Btree-ben minden csomópontnak legalább két ága van, és mindegyik csomópont tartalmaz néhány rekordot, így nem kell a levél csomópontjaiig bejárnunk az adatok megszerzéséhez. | A B+ fában a belső csomópontok csak mutatókat, a levélcsomópontok pedig rekordokat tartalmaznak. Az összes levélcsomópont ugyanazon a szinten van, így a levélcsomópontokig kell bejárnunk, hogy megkapjuk az adatokat. |
| A gyökércsomópont legalább 2-m gyermeket tartalmaz, ahol m a fa sorrendje. | A gyökércsomópont legalább 2-m gyermeket tartalmaz, ahol m a fa sorrendje. |
