A verem egy lineáris adatstruktúra, amely követi a LIFO (Last-In-First-Out) elv. A veremnek egy vége van, míg a sornak két vége van ( elől és hátul ). Csak egy mutatót tartalmaz felső mutató a verem legfelső elemére mutatva. Amikor egy elemet hozzáadunk a veremhez, az a verem tetejére kerül, és az elem csak a veremből törölhető. Más szóval, a A verem egy olyan tárolóként definiálható, amelyben a beillesztés és a törlés a verem tetejeként ismert egyik végéről történhet.

Néhány kulcsfontosságú pont a veremhez kapcsolódóan

• Veremnek hívják, mert úgy viselkedik, mint egy valós halom, könyvhalmok stb.
• A Stack egy előre meghatározott kapacitású absztrakt adattípus, ami azt jelenti, hogy korlátozott méretű elemeket képes tárolni.
• Ez egy olyan adatstruktúra, amely bizonyos sorrendet követ az elemek beszúrásához és törléséhez, és ez a sorrend lehet LIFO vagy FILO.

A Stack működése

A verem a LIFO mintán működik. Amint az alábbi ábrán láthatjuk, a veremben öt memóriablokk található; ezért a köteg mérete 5.

karaktert karakterláncra java-ban

Tegyük fel, hogy az elemeket egy veremben akarjuk tárolni, és tegyük fel, hogy a verem üres. A lent látható módon vettük az 5-ös méretű köteget, amelyben egyenként tologatjuk az elemeket, amíg a köteg meg nem telik.

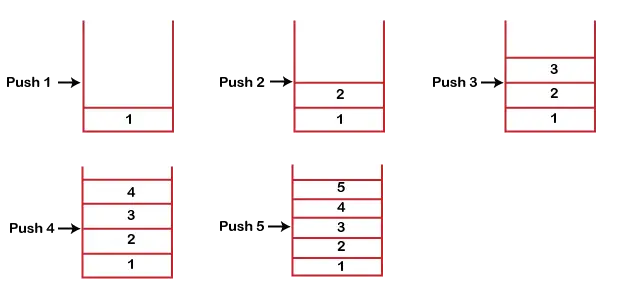
Mivel a veremünk tele van, a verem mérete 5. A fenti esetekben megfigyelhető, hogy felülről lefelé halad, amikor az új elemet a verembe adtuk be. A köteg alulról felfelé töltődik.

Amikor végrehajtjuk a törlési műveletet a veremen, csak egy mód van a be- és kilépésre, mivel a másik vége zárva van. A LIFO mintát követi, ami azt jelenti, hogy az elsőként megadott érték törlődik utoljára. A fenti esetben először az 5-ös értéket adjuk meg, így az csak az összes többi elem törlése után kerül eltávolításra.

Szabványos veremműveletek

Az alábbiakban néhány általános műveletet találunk a veremben:

nyom():Amikor egy elemet beszúrunk egy verembe, akkor a műveletet push-nak nevezzük. Ha a verem megtelt, akkor túlcsordulási állapot lép fel.pop():Amikor törölünk egy elemet a veremből, a műveletet pop-nak nevezzük. Ha a verem üres, azt jelenti, hogy nincs elem a veremben, ezt az állapotot alulcsordulási állapotnak nevezzük.üres():Meghatározza, hogy a verem üres-e vagy sem.tele van():Ez határozza meg, hogy a verem megtelt-e vagy sem.kandikál():Visszaadja az elemet az adott pozícióban.számol():A veremben elérhető elemek teljes számát adja vissza.változás():Megváltoztatja az elemet az adott helyen.kijelző():Kinyomtatja a veremben elérhető összes elemet.

PUSH működés

A PUSH művelet lépései az alábbiak:

• Mielőtt egy elemet beszúrnánk egy verembe, ellenőrizzük, hogy a verem megtelt-e.
• Ha az elemet egy verembe próbáljuk beilleszteni, és a verem megtelt, akkor a túlcsordulás állapot lép fel.
• Amikor inicializálunk egy veremet, a top értékét -1-re állítjuk, hogy ellenőrizzük, hogy a verem üres-e.
• Amikor az új elemet egy verembe tolják, először a felső értéke növekszik, azaz top=top+1, és az elem az új pozícióba kerül tetejére .
• Az elemek addig lesznek beszúrva, amíg el nem érjük a max a verem mérete.

POP működés

A POP művelet lépései az alábbiak:

np pont

• Mielőtt törölnénk az elemet a veremből, ellenőrizzük, hogy a verem üres-e.
• Ha megpróbáljuk törölni az elemet az üres veremből, akkor a alulfolyó állapot lép fel.
• Ha a verem nem üres, először elérjük azt az elemet, amelyre a tetejére
• A pop művelet végrehajtása után a felső 1-gyel csökken, azaz top=top-1 .

A Stack alkalmazásai

A verem alkalmazásai a következők:

A szimbólumok egyensúlya:A verem egy szimbólum egyensúlyozására szolgál. Például a következő programunk van:

 int main() { cout&lt;<'hello'; cout<<'javatpoint'; } < pre> <p>As we know, each program has <em>an opening</em> and <em>closing</em> braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.</p> <ul> <tr><td>String reversal:</td> Stack is also used for reversing a string. For example, we want to reverse a &apos; <strong>javaTpoint</strong> &apos; string, so we can achieve this with the help of a stack. <br> First, we push all the characters of the string in a stack until we reach the null character. <br> After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack. </tr><tr><td>UNDO/REDO:</td> It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write &apos;a&apos;, then &apos;b&apos;, and then &apos;c&apos;; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state. <br> If we want to perform UNDO operation, and want to achieve &apos;ab&apos; state, then we implement pop operation. </tr><tr><td>Recursion:</td> The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained. </tr><tr><td>DFS(Depth First Search):</td> This search is implemented on a Graph, and Graph uses the stack data structure. </tr><tr><td>Backtracking:</td> Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure. </tr><tr><td>Expression conversion:</td> Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below: <pre>Infix to prefix Infix to postfix Prefix to infix Prefix to postfix Postfix to infix</pre> </tr><tr><td>Memory management:</td> The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released. </tr></ul> <hr></'hello';>