Ebben a részben az NFA ekvivalens DFA-vá alakításának módszerét tárgyaljuk. Az NFA-ban, amikor egy adott bemenetet adunk az aktuális állapothoz, a gép több állapotba kerül. Egy adott bemeneti szimbólumon lehet nulla, egy vagy több mozdulat. Másrészt a DFA-ban, amikor egy adott bemenetet adunk az aktuális állapothoz, a gép csak egy állapotba kerül. A DFA-nak csak egy lépése van egy adott bemeneti szimbólumon.
Legyen M = (Q, ∑, δ, q0, F) olyan NFA, amely elfogadja az L(M) nyelvet. Egyenértékű DFA-nak kell lennie, amelyet M' = (Q', ∑', q0', δ', F') jelölünk úgy, hogy L(M) = L(M').
Az NFA DFA-vá alakításának lépései:
1. lépés: Kezdetben Q' = ϕ
2. lépés: Adja hozzá q0 NFA-t a Q'-hez. Ezután keresse meg az átmeneteket ebből a kezdőállapotból.
3. lépés: A Q'-ban keresse meg az egyes bemeneti szimbólumok lehetséges állapotkészletét. Ha ez az állapothalmaz nincs Q'-ben, akkor adja hozzá a Q'-hez.
4. lépés: A DFA-ban a végső állapot minden olyan állapot lesz, amely tartalmazza az F-t (NFA végső állapotai)
1. példa:
Konvertálja az adott NFA-t DFA-vá.
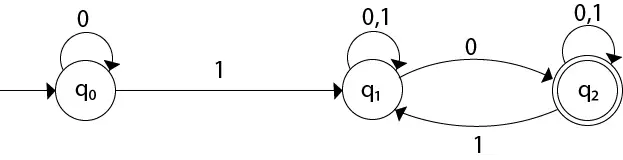
Megoldás: Az adott átmenet diagramhoz először elkészítjük az átmeneti táblát.
| Állapot | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Most megkapjuk a δ' átmenetet a q0 állapothoz.
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
A q1 állapot δ' átmenetét a következőképpen kapjuk meg:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
A q2 állapot δ' átmenetét a következőképpen kapjuk meg:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Most megkapjuk a δ' átmenetet [q1, q2]-n.
nat vs ágy
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] A [q1, q2] állapot egyben a végső állapot is, mert tartalmaz egy q2 végállapotot. Az elkészített DFA átmeneti táblázata a következő lesz:
| Állapot | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
Az átmenet diagram a következő lesz:

A q2 állapot kiküszöbölhető, mert q2 elérhetetlen állapot.
2. példa:
Konvertálja az adott NFA-t DFA-vá.

Megoldás: Az adott átmenet diagramhoz először elkészítjük az átmeneti táblát.
| Állapot | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Most megkapjuk a δ' átmenetet a q0 állapothoz.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] A q1 állapot δ' átmenetét a következőképpen kapjuk meg:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Most megkapjuk a δ' átmenetet [q0, q1]-en.
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] Hasonlóképpen,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Ahogy az adott NFA-ban a q1 egy végső állapot, akkor a DFA-ban, ahol q1 létezik, ez az állapot végső állapottá válik. Ezért a DFA-ban a végső állapotok [q1] és [q0, q1]. Ezért az F = {[q1], [q0, q1]} végállapotok halmaza.
Az elkészített DFA átmeneti táblázata a következő lesz:
| Állapot | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
Az átmenet diagram a következő lesz:

Még a DFA állapotainak nevét is megváltoztathatjuk.
Tegyük fel
A = [q0] B = [q1] C = [q0, q1]
Ezekkel az új nevekkel a DFA a következő lesz:

