A matematika egy lenyűgöző tantárgy, amely fogalmak és alapelvek széles skálájából áll; az egyik ilyen fogalom exponenciális jelölés . Az exponenciális jelölés egy olyan alapvető fogalom, amely magában foglalja az alapszámnak egy adott hatványra (vagy kitevőre) emelését. Ez egy erőteljes fogalom, amelyet a hatalmas és minimális számok megfelelőbb kifejezésére használnak; egy ilyen példát tárgyalunk ebben a cikkben, azaz 10-től 5-ig^thErő. Tehát ebben a cikkben megismerjük az exponenciális jelölés fogalmát, megvitatjuk a 10 és az 5 közötti jelentőségét.^thHatalom, ismerje meg ennek az értéknek a kifejezésének különféle módjait, és vitassa meg az exponenciális jelölés alkalmazásait a matematikán kívül más területeken is.

Exponenciális jelölés meghatározása

Az exponenciális vagy tudományos jelölés szabványos és szervezett módszert biztosít a számok ábrázolására. Előnyös, ha nagy és kis számokkal foglalkozunk, mivel leegyszerűsíti kifejezésüket és javítja az áttekinthetőséget.

A tudományos jelölés részei

Ennek a jelölésnek két része van:

1. Az alapszám
2. A kitevő (vagy hatvány) szám

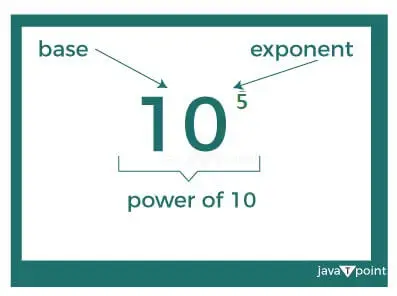
Az alap 10, a kitevő pedig 5, ami azt mutatja, hogy az alapszám (10) hányszorosára szorozzuk meg önmagával; ez arra utal 10 az 5 hatványához egyenlő 10-zel, 5-ször szorozva önmagával .

10 x 10 x 10 x 10 x 10 = 10⁵

10-et kifejezve 5-re^thErő

Sokféleképpen lehet kifejezni vagy képviselni a 10-et az 5. Hatalomig, ami attól is függ, hogy milyen területen használják, vagy a személyes preferenciáktól függ.

Tudományos jelöléssel:A legegyszerűbb ábrázolás a 10⁵, ahol 10 bázis, 5 pedig kitevő vagy hatvány; ez a formátum általában érthető, és gyakran használják a matematikai és tudományos irodalomban.Számszerű ábrázolás:Egy másik módja annak, hogy a 10-et az 5 hatványával fejezzük ki, ha a számot kibővített formában, 100 000-ben írjuk le. Ez a formátum a számot számjegyekre bontja, és kiemeli annak nagyságát, hogy megértse a jelentőségét.Hosszú alak:A 10 hosszú formátumú ábrázolása az 5 erejéig „egy lakh”, ezt a formátumot használjuk mindennapi nyelvünkön, így könnyebben megérthetjük a számot.

Jelentős

10-től 5-ig^thA hatalom nagyon fontos volt különböző területeken, elsősorban a tudományos kutatásban, a technológiában és a mindennapi életben; ez egy lakh értékét jelenti, ami egyenlő 1-gyel, amelyet öt nulla követ, azaz 100 000. A tudományos jelölésekben ezt az értéket gyakran használják hatalmas mennyiségek mérésekor, például a bolygók és az égi objektumok távolságát, az univerzumban lévő csillagok számát és a világ népességét. Segíti a tudósokat és a kutatókat abban, hogy könnyebben kifejezzék ezeket a nagyon nagy mennyiségeket, és kényelmesebbé teszi számukra az adatok megértését és elemzését.

Jelentkezések 10-től 5-ig^thErő

Most, hogy megértettük a számítást, vizsgáljunk meg néhány gyakorlati alkalmazást, ahol megtalálhatjuk a 10 és az 5 közötti relevanciát.^thErő:

Digitális technológia:A számítógépekben és a digitális technológiában a 10-es hatványok jelentős szerepet játszanak. A számítógépek kétjegyű rendszeren (0 és 1) alapuló bináris kód segítségével tárolják és dolgozzák fel az információkat. A 2 hatványai, amelyek szorosan kapcsolódnak a 10-hez, a memóriakártya méretét, az adatátviteli sebességet és a processzorok sebességét jelzik.Népesség növekedés:Exponenciális növekedés gyakran megfigyelhető a természeti jelenségekben, beleértve a népességnövekedést is. A 10-től az 5-ig koncepció^thA hatalom segíthet megértenünk, hogyan növekedhet gyorsan a népesség az idő múlásával; Például, ha egy 100 000 egyedből álló populáció évi 10%-os ütemben növekszik, akkor négy év múlva megközelítőleg 14 6410-et érne el.Tudományos jelöléssel:10-től 5-ig^thA hatalom a tudományos jelölés döntő összetevője. Ez a jelölés nagyon nagy vagy minimális számokat fejez ki jobban kezelhető formátumban.Skála és nagyságrend:A 10-es hatványokat gyakran használják a tárgyak vagy jelenségek hatalmasságának vagy apróságának leírására. Például a csillagászok a fényév fogalmát használják, ami az a távolság, amelyet a fény egy év alatt megtesz.Nagy számok számítása:Az olyan területeken, mint a pénzügy, a fizika és a mérnöki tudomány, általában nagy numerikus számításokat kell végezni. Az exponenciális jelölés értékes ezeknek a számításoknak az egyszerűsítésében, mivel lehetővé teszi a kompakt ábrázolást és csökkenti a hibalehetőséget.

Következtetés

A hatványozás megértése elengedhetetlen készség a különféle hatványokra emelt számok kifejezéséhez. Ebben a cikkben megvizsgáltuk, hogyan lehet 10-et 5-höz kifejezni^thHatalom, ami azt jelenti, hogy 10-zel ötször megszorozzuk; az eredmény, a 100 000, egy alapvető érték, amely különböző kontextusokban jelenik meg, mint például a tudományos jelölésekben, az egységek konvertálásában és a kettes számrendszerekben. Az exponenciális jelölés fogalmának és gyakorlati alkalmazásainak megismerésével jobban megérthetjük a matematika Erejét és bőségét (jelenlétét) a mindennapi életben.