- A lenyomó automaták a CFG megvalósításának egyik módja, ugyanúgy, ahogy a DFA-t egy normál nyelvtanhoz tervezzük. Egy DFA véges mennyiségű információra képes megjegyezni, de egy PDA végtelen mennyiségű információra képes megjegyezni.
- A lenyomó automaták egyszerűen egy NFA, amelyet „külső veremmemóriával” egészítenek ki. A verem hozzáadásával a Pushdown automaták „utoljára az elsőben” memóriakezelési képességet biztosítják. A lenyomó automaták korlátlan mennyiségű információt tárolhatnak a veremben. Korlátozott mennyiségű információhoz férhet hozzá a veremben. A PDA képes egy elemet a verem tetejére tolni, és kipattanni egy elemet a verem tetejéről. Ahhoz, hogy egy elemet beolvassunk a verembe, a felső elemeket le kell ugrani, és elvesznek.
- A PDA erősebb, mint az FA. Bármely nyelv, amelyet az FA elfogad, elfogadható lehet a PDA számára is. A PDA egy olyan nyelvosztályt is elfogad, amelyet még az FA sem fogad el. Így a PDA sokkal jobb, mint az FA.
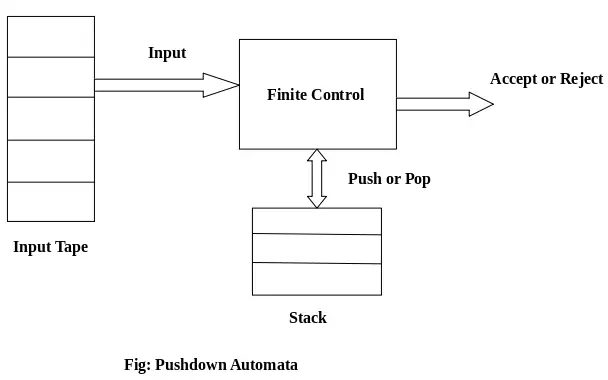
PDA komponensek:
Bemeneti szalag: A bemeneti szalag sok cellára vagy szimbólumra van felosztva. A beviteli fej csak olvasható, és csak egy szimbólumot mozgathat balról jobbra.
Véges vezérlés: A véges vezérlőnek van néhány mutatója, amely az aktuális beolvasandó szimbólumra mutat.
Kazal: A verem egy olyan szerkezet, amelyben csak az egyik végéről tudjuk tolni és kivenni a tárgyakat. Mérete végtelen. A PDA-ban a verem az elemek ideiglenes tárolására szolgál.
A PDA hivatalos meghatározása:
A PDA 7 komponens gyűjteményeként határozható meg:
K: az állapotok véges halmaza
∑: a bemeneti készlet
C: egy verem szimbólum, amelyet el lehet tolni és ki lehet emelni a veremből
q0: a kezdeti állapot
autocad stretch parancs
VAL VEL: egy kezdő szimbólum, amely Γ-ben van.
F: végső állapotok halmaza
d: leképezési funkció, amely az aktuális állapotból a következő állapotba való átlépéshez használható.
Azonnali leírás (azonosító)
Az azonosító egy informális jelölés arra vonatkozóan, hogy a PDA hogyan számítja ki a bemeneti karakterláncot, és hogyan dönt a karakterlánc elfogadása vagy elutasítása mellett.
A pillanatnyi leírás egy hármas (q, w, α), ahol:
q az aktuális állapotot írja le.
Ban ben leírja a fennmaradó bemenetet.
katódsugárcsöves monitor
a leírja a verem tartalmát, bal felső sarokban.
Forgóajtó jelölése:
⊢ jel leírja a forgókapu jelölését és egy mozdulatot jelent.
⊢* jel egy mozdulatsort ír le.
Például,
(p, b, T) ⊢ (q, w, α)
react inline stílusban
A fenti példában a p állapotból a q-ba történő átmenet során a „b” bemeneti szimbólum felhasználásra kerül, és a „T” verem tetejét egy új α karakterlánc képviseli.
1. példa:
Nyelv fogadására alkalmas PDA tervezése anb2n.
Megoldás: Ebben a nyelvben n számú a-t 2n számú b-nek kell követnie. Ezért egy nagyon egyszerű logikát fogunk alkalmazni, vagyis ha egyetlen 'a'-t olvasunk, akkor két a-t fogunk a verembe tolni. Amint elolvassuk a „b”-t, akkor minden egyes „b”-hez csak egy „a” kerüljön ki a veremből.
Az azonosító a következőképpen állítható fel:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Most, amikor olvassuk a b-t, az állapotot q0-ról q1-re változtatjuk, és elkezdjük a megfelelő 'a'-t. Ennélfogva,
δ(q0, b, a) = (q1, ε)
Így a „b” felbukkanásának folyamata megismétlődik, hacsak nem olvassa el az összes szimbólumot. Vegye figyelembe, hogy a felbukkanó művelet csak q1 állapotban történik.
δ(q1, b, a) = (q1, ε)
Az összes b kiolvasása után az összes megfelelő a-nak fel kell bukkannia. Ezért amikor ε-t olvasunk bemeneti szimbólumként, akkor semmi sem lehet a veremben. A lépés tehát a következő lesz:
δ(q1, ε, Z) = (q2, ε)
Ahol
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Az azonosítót így foglalhatjuk össze:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Most ezt a PDA-t szimuláljuk az „aaabbbbbb” bemeneti karakterlánchoz.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
2. példa:
Tervezzen egy PDA-t a 0 nyelv fogadásáran1m0n.
Megoldás: Ebben a PDA-ban n számú 0 után tetszőleges számú 1, majd n számú 0 követi. Ezért az ilyen PDA tervezésének logikája a következő lesz:
Ha az első 0-val találkozik, helyezze az összes 0-t a verembe. Aztán ha elolvassuk az 1-et, ne csináljunk semmit. Ezután olvassa el a 0-t, és a 0 minden leolvasásakor emeljen ki egy 0-t a veremből.
java egyenlő módszer
Például:

Ez a forgatókönyv a következőképpen írható be az azonosító űrlapba:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Most ezt a PDA-t szimuláljuk a „0011100” bemeneti karakterlánchoz.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
