• A Naív Bayes algoritmus egy felügyelt tanulási algoritmus, amely a Bayes-tétel és osztályozási problémák megoldására használják.
• Főleg ben használják szöveges besorolás amely egy nagy dimenziós képzési adatkészletet tartalmaz.
• A Naive Bayes Classfier az egyik egyszerű és leghatékonyabb osztályozási algoritmus, amely segít a gyors előrejelzéseket lehetővé tevő gyors gépi tanulási modellek felépítésében.
Ez egy valószínűségi osztályozó, ami azt jelenti, hogy egy objektum valószínűsége alapján jósol.
• Néhány népszerű példa a Naív Bayes algoritmusra spamszűrés, szentimentális elemzés és cikkek osztályozása .

Miért hívják Naív Bayesnek?

A Naive Bayes algoritmus két Naív és Bayes szóból áll, amelyek a következőképpen írhatók le:

Naiv: Naívnak nevezik, mert feltételezi, hogy egy bizonyos jellemző előfordulása független más jellemzők előfordulásától. Például ha a gyümölcsöt szín, forma és íz alapján azonosítják, akkor a piros, gömb alakú és édes gyümölcsöt almának ismerik el. Ezért minden egyes jellemző külön-külön hozzájárul ahhoz, hogy azonosítsuk, hogy almáról van szó, anélkül, hogy egymástól függnének.Bayes: Bayes-nek hívják, mert ez a Bayes-tétel elvétől függ.

Bayes-tétel:

• Bayes tétele más néven Bayes szabálya vagy Bayes törvénye , amely egy hipotézis valószínűségének meghatározására szolgál előzetes tudással. Ez a feltételes valószínűségtől függ.
• A Bayes-tétel képlete a következő:

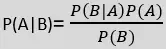
Ahol,

P(A|B) a posterior valószínűség : Az A hipotézis valószínűsége a B megfigyelt eseményre vonatkozóan.

P(B|A) a valószínűség valószínűsége : Annak a bizonyítéknak a valószínűsége, hogy egy hipotézis valószínűsége igaz.

P(A) az előzetes valószínűség : A hipotézis valószínűsége a bizonyítékok megfigyelése előtt.

P(B) a határvalószínűség : Bizonyíték valószínűsége.

A Naive Bayes osztályozójának működése:

A Naive Bayes osztályozójának működése az alábbi példa segítségével érthető meg:

Tegyük fel, hogy van egy adatkészletünk időjárási viszonyok és a megfelelő célváltozó Játék '. Tehát ennek az adathalmaznak a segítségével el kell döntenünk, hogy az időjárási viszonyoknak megfelelően egy adott napon játszunk-e vagy sem. Tehát a probléma megoldásához az alábbi lépéseket kell követnünk:

1. Konvertálja a megadott adatkészletet gyakorisági táblázatokká.
2. Valószínűségi táblázat létrehozása adott jellemzők valószínűségének megkeresésével.
3. Most használja a Bayes-tételt a posterior valószínűség kiszámításához.

Probléma : Ha napos az idő, akkor a Player játszhat vagy sem?

Megoldás : Ennek megoldásához először vegye figyelembe az alábbi adatkészletet:

Gyakorisági táblázat az időjárási viszonyokhoz:

Valószínűségi táblázat időjárási viszonyok:

Bayes-tétel alkalmazása:

P(igen|napos)= P(napos|igen)*P(igen)/P(napos)

P(napos|Igen)= 3/10= 0,3

P(napos)= 0,35

P(Igen)=0,71

Tehát P(igen|napos) = 0,3*0,71/0,35= 0,60

P(nem|napos)= P(napos|nem)*P(nem)/P(napos)

P(napos|NO)= 2/4=0,5

P(nem)=0,29

P(napos)= 0,35

java arraylist rendezés

Tehát P(nem|napos)= 0,5*0,29/0,35 = 0,41

Tehát amint a fenti számításból láthatjuk, hogy P(igen|napos)>P(nem|napos)

Így egy napsütéses napon a játékos játszhat a játékkal.

A Naive Bayes osztályozó előnyei:

• A Naïve Bayes az egyik gyors és egyszerű ML algoritmus az adatkészletek osztályának előrejelzésére.
• Használható bináris és több osztályú osztályozáshoz is.
• A többi algoritmushoz képest jól teljesít a többosztályú előrejelzésekben.
• Ez a legnépszerűbb választás szövegbesorolási problémák .

A Naive Bayes osztályozó hátrányai:

• A naiv Bayes azt feltételezi, hogy minden jellemző független vagy független, így nem tudja megtanulni a tulajdonságok közötti kapcsolatot.

A Naive Bayes osztályozó alkalmazásai:

• Arra használják Credit Scoring .
• -ben használják orvosi adatok osztályozása .
• Használható benne valós idejű előrejelzések mert a Naive Bayes Classifier lelkes tanuló.
• Szöveges osztályozásban használatos, mint pl Spam szűrés és Érzelemelemzés .

A naiv Bayes-modell típusai:

A Naive Bayes-modellnek három típusa van, amelyeket alább mutatunk be:

Gauss-féle: A Gauss-modell feltételezi, hogy a jellemzők normális eloszlást követnek. Ez azt jelenti, hogy ha a prediktorok folytonos értékeket vesznek fel diszkrét helyett, akkor a modell azt feltételezi, hogy ezek az értékek a Gauss-eloszlásból vannak mintavételezve.Multinomiális: A Multinomial Naive Bayes osztályozó akkor használatos, ha az adatok többnomiális elosztásúak. Elsősorban dokumentum-besorolási problémákra használják, ez azt jelenti, hogy egy adott dokumentum melyik kategóriába tartozik, például sport, politika, oktatás stb.
Az osztályozó a szavak gyakoriságát használja a prediktorokhoz.Bernoulli: A Bernoulli osztályozó a Multinomiális osztályozóhoz hasonlóan működik, de a prediktor változók a független Boole-változók. Például, hogy egy adott szó jelen van-e egy dokumentumban vagy nincs. Ez a modell a dokumentumosztályozási feladatokról is híres.

A Naive Bayes algoritmus Python implementációja:

Most egy naiv Bayes algoritmust fogunk megvalósítani Python használatával. Tehát ehhez a ' felhasználói adat ' adatkészlet , amelyet másik osztályozási modellünkben is használtunk. Így a Naive Bayes modell könnyen összehasonlítható a többi modellel.

A megvalósítás lépései:

• Adatok előfeldolgozási lépése
• Naive Bayes illesztése az edzéskészlethez
• A teszt eredményének előrejelzése
• Az eredmény tesztelési pontossága (zavaros mátrix létrehozása)
• A tesztkészlet eredményének megjelenítése.

1) Adat-előfeldolgozási lépés:

Ebben a lépésben előfeldolgozzuk/előkészítjük az adatokat, hogy azokat hatékonyan tudjuk felhasználni a kódunkban. Hasonló, mint az adat-előfeldolgozásnál. Ennek kódja az alábbiakban található:

nginx

 Importing the libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd # Importing the dataset dataset = pd.read_csv('user_data.csv') x = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values # Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0) # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() x_train = sc.fit_transform(x_train) x_test = sc.transform(x_test) 

A fenti kódban az adatkészletet a programunkba a ' dataset = pd.read_csv('user_data.csv') . A betöltött adatkészlet képzési és tesztkészletre van felosztva, majd átméreteztük a jellemző változót.

Az adatkészlet kimenete a következő:

2) Naive Bayes felszerelése az edzőkészlethez:

Az előfeldolgozási lépés után most a Naive Bayes modellt illesztjük a Training készlethez. Alább található a kódja hozzá:

 # Fitting Naive Bayes to the Training set from sklearn.naive_bayes import GaussianNB classifier = GaussianNB() classifier.fit(x_train, y_train) 

A fenti kódban a GaussianNB osztályozó hogy illeszkedjen a képzési adatkészlethez. Más osztályozókat is használhatunk igényünk szerint.

Kimenet:

 Out[6]: GaussianNB(priors=None, var_smoothing=1e-09) 

3) A tesztsorozat eredményének előrejelzése:

Most megjósoljuk a tesztkészlet eredményét. Ehhez létrehozunk egy új prediktor változót y_pred , és a predikció függvényt fogja használni az előrejelzésekhez.

 # Predicting the Test set results y_pred = classifier.predict(x_test) 

Kimenet:

A fenti kimenet a predikciós vektor eredményét mutatja y_pred és valós vektor y_teszt. Láthatjuk, hogy egyes predikációk eltérnek a valós értékektől, amelyek a hibás előrejelzések.

4) Zavart mátrix létrehozása:

Most ellenőrizzük a Naive Bayes osztályozó pontosságát a Confusion mátrix segítségével. Alább található a kódja hozzá:

 # Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) 

Kimenet:

Amint azt a fenti zavaros mátrix kimenetben láthatjuk, 7+3=10 helytelen és 65+25=90 helyes előrejelzés létezik.

5) Az edzéssorozat eredményének megjelenítése:

Ezután a Na�ve Bayes osztályozó segítségével vizualizáljuk az edzési sorozat eredményét. Alább található a kódja hozzá:

 # Visualising the Training set results from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Kimenet:

A fenti kimenetben láthatjuk, hogy a Na�ve Bayes osztályozó az adatpontokat a finom határvonallal elkülönítette. Ez a Gauss-görbe, ahogyan mi is használtuk GaussianNB osztályozó a kódunkban.

6) A tesztkészlet eredményének megjelenítése:

 # Visualising the Test set results from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Kimenet:

A fenti kimenet a tesztkészlet adatok végső kimenete. Amint látjuk, az osztályozó Gauss-görbét hozott létre a „vásárolt” és a „nem vásárolt” változók felosztására. Vannak hibás előrejelzések, amelyeket a Confusion mátrixban számoltunk ki. De így is nagyon jó osztályozó.