A kifejezésfa a különböző kifejezések reprezentálására szolgáló fa. A fa adatstruktúra az expressziós utasítások ábrázolására szolgál. Ebben a fában a belső csomópont mindig az operátorokat jelöli.
- A levél csomópontjai mindig az operandusokat jelölik.
- A műveleteket mindig ezeken az operandusokon hajtják végre.
- A fa mélyén jelenlévő kezelő mindig a legmagasabb prioritást élvezi.
- Az operátor, amely nem nagyon van a fában a mélyben, mindig a legalacsonyabb prioritást élvezi a mélyben fekvő operátorokhoz képest.
- Az operandus mindig a fa mélyén jelenik meg; ezért tekinthető a legfontosabb az összes üzemeltető között.
- Röviden úgy foglalhatjuk össze, hogy a fa mélyén jelenlévő érték a legmagasabb prioritású a fa tetején lévő többi operátorhoz képest.
- Ezeknek a kifejezési fáknak a fő használata az, hogy megszokták értékelni, elemezni és módosít a különféle kifejezéseket.
- A kifejezésben szereplő egyes operátorok asszociativitásának kiderítésére is szolgál.
- Például a + operátor a baloldali asszociatív, a / pedig a jobb oldali asszociatív.
- Az asszociativitás dilemmáját a kifejezési fák segítségével tisztáztuk.
- Ezeket a kifejezési fákat környezetfüggetlen nyelvtan segítségével alakítjuk ki.
- Minden nyelvtani produkció elé egy szabályt társítottunk a környezetfüggetlen nyelvtanokban.
- Ezeket a szabályokat szemantikai szabályoknak is nevezik, és ezeknek a szemantikai szabályoknak a használatával könnyen létrehozhatjuk a kifejezésfákat.
- Ez a fordítóprogram tervezésének egyik fő része, és a szemantikai elemzés fázisához tartozik.
- Ebben a szemantikai elemzésben a szintaxis-irányított fordításokat fogjuk használni, és kimenet formájában elkészítjük a megjegyzésekkel ellátott értelmezőfát.
- A megjegyzésekkel ellátott elemzési fa nem más, mint a type attribútumhoz és az egyes termelési szabályokhoz társított egyszerű elemzés.
- A kifejezésfák használatának fő célja összetett kifejezések létrehozása, amelyek könnyen kiértékelhetők ezekkel a kifejezési fákkal.
- Megváltoztathatatlan, és miután létrehoztunk egy kifejezésfát, nem tudjuk megváltoztatni vagy tovább módosítani.
- További módosításokhoz az új kifejezésfát teljes egészében meg kell alkotni.
- A postfix, prefix és infix kifejezések kiértékelésének megoldására is használható.
A kifejezőfák nagyon fontos szerepet játszanak a nyelvi szintű kódot az adatok formájában, amelyeket főként a faszerű struktúrában tárolunk. Azt is használják a memória reprezentációjában lambda kifejezés. A fa adatstruktúra segítségével átláthatóbban és explicitebben tudjuk kifejezni a lambda kifejezést. Először úgy jön létre, hogy a kódszegmenst adatszegmenssé konvertálja, hogy a kifejezés könnyen kiértékelhető legyen.
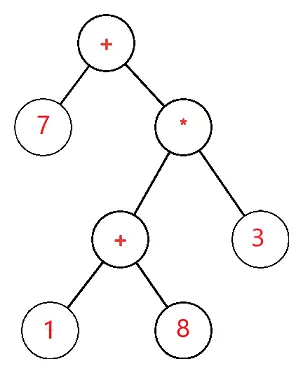
A kifejezésfa egy bináris fa, amelyben minden külső vagy levélcsomópont megfelel az operandusnak, és minden belső vagy szülőcsomópont megfelel az operátoroknak, így például a 7 + ((1+8)*3) kifejezésfa a következő lenne:
Legyen S a kifejezésfa
Ha S nem nulla, akkor
Ha az S.value egy operandus, akkor
S.érték visszatérése
x = megold (S.bal)
y = megold (S.jobb)
Visszatérési számítás(x, y, S.érték)
A fenti példában a kifejezésfa környezetfüggetlen nyelvtant használt.
Ebben a nyelvtanban van néhány produkció, amely bizonyos termelési szabályokhoz kapcsolódik, főként ún szemantikai szabályok . E szemantikai szabályok segítségével meghatározhatjuk az eredmény-előállítást a megfelelő termelési szabályokból. Itt az érték paramétert használtuk, amely kiszámítja az eredményt, és visszaadja a nyelvtan kezdőszimbólumához. Az S.left kiszámítja a csomópont bal gyermekét, és hasonlóképpen a csomópont jobb gyermeke is kiszámítható az S.right paraméterrel.
Kifejezési fa használata
- A kifejezésfák használatának fő célja összetett kifejezések létrehozása, amelyek könnyen kiértékelhetők ezekkel a kifejezési fákkal.
- A kifejezésben szereplő egyes operátorok asszociativitásának kiderítésére is szolgál.
- A postfix, prefix és infix kifejezések kiértékelésének megoldására is használható.
Kifejezési fa megvalósítása
A kifejezésfa megvalósításához és programjának megírásához verem adatszerkezetet kell használnunk.
Mint tudjuk, hogy a verem a legutolsó az elsőben LIFO elven alapul, a verembe nemrég betolt adatelem szükség esetén ki lett ugorva. Ennek megvalósításához a verem két fő műveletét, a push-ot és a pop-ot használjuk. A push művelettel az adatelemet a verembe toljuk, a pop művelettel pedig eltávolítjuk az adatelemet a veremből.
A verem fő funkciói a kifejezésfa megvalósításában:
Először az adott kifejezést balról jobbra szkenneljük, majd egyesével ellenőrizzük az azonosított karaktert,
- Ha egy beolvasott karakter operandus, akkor a push műveletet alkalmazzuk, és a verembe toljuk.
- Ha egy beolvasott karakter operátor, akkor a pop műveletet alkalmazzuk benne, hogy eltávolítsuk a két értéket a veremből, hogy gyermekei legyenek, majd ezután visszatoljuk az aktuális szülőcsomópontot a verembe.
Kifejezési fa megvalósítása C programozási nyelven
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> A fenti program kimenete:
X + Y * Z / W
Kifejezési fa megvalósítása C++ programozási nyelven
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> A fenti program kimenete:
X + Y * Z / W
Kifejezési fa megvalósítása Java programozási nyelven
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 