- A DFA determinisztikus véges automatákra utal. A determinisztikus a számítás egyediségére utal. A véges automatákat determinisztikus véges automatáknak nevezzük, ha a gép egy bemeneti sztringet egy-egy szimbólummal olvas be.
- A DFA-ban csak egy útvonal van az adott bemenethez az aktuális állapotból a következő állapotba.
- A DFA nem fogadja el a nullmozgást, azaz a DFA nem tud állapotot változtatni bemeneti karakter nélkül.
- A DFA több végső állapotot is tartalmazhat. A Compiler Lexical Analysisben használatos.
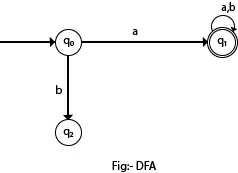
A következő ábrán láthatjuk, hogy a q0 állapotból az a bemenethez csak egy út vezet a q1-hez. Hasonlóképpen, q0-ból csak egy út van a b bemenet számára, amely a q2-be megy.
A DFA formális meghatározása
A DFA az FA definíciójában leírtakkal megegyező 5 sorból álló gyűjtemény.
tömbök java
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Az átmenet függvény a következőképpen definiálható:
δ: Q x ∑→Q
A DFA grafikus ábrázolása
A DFA-t állapotdiagramnak nevezett digráfokkal ábrázolhatjuk. Amiben:
- Az állapotot csúcsok képviselik.
- A bemeneti karakterrel jelölt ív mutatja az átmeneteket.
- A kezdeti állapotot nyíl jelzi.
- A végső állapotot kettős kör jelöli.
1. példa:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Megoldás:
Átmeneti diagram:

Átmeneti táblázat:
sor és oszlop
| Jelen állapot | A 0. bemenet következő állapota | Következő 1. beviteli állapot |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
2. példa:
A ∑ = {0, 1} értékkel rendelkező DFA minden 0-val kezdődőt elfogad.
Megoldás:

Magyarázat:
pothineni ram
- A fenti ábrán láthatjuk, hogy adott 0-nál a DFA bemeneteként a q0 állapotban a DFA állapotát q1-re változtatja, és mindig a q1 végső állapotba megy a 0-s bemenet indításakor. Elfogadhat 00, 01, 000, 001... .stb. Nem tud elfogadni egyetlen 1-gyel kezdődő karakterláncot sem, mert soha nem kerül végső állapotba az 1-gyel kezdődő karakterláncon.
3. példa:
A ∑ = {0, 1} értékkel rendelkező DFA elfogad minden 0-ra végződőt.
Megoldás:

Magyarázat:
A fenti diagramon láthatjuk, hogy adott 0-nál a DFA bemeneteként q0 állapotban a DFA állapotát q1-re változtatja. Bármilyen 0-ra végződő karakterláncot el tud fogadni, például 00, 10, 110, 100... stb. Nem tud elfogadni olyan karakterláncot, amely 1-re végződik, mert 1 bemeneten soha nem megy a q1 végső állapotba, így az 1-re végződő karakterláncot nem fogadja el, vagy elutasítja.
