A Törlés funkció a megadott csomópont törlésére szolgál a bináris keresési fából. A bináris keresési fából azonban egy csomópontot úgy kell törölnünk, hogy a bináris keresési fa tulajdonsága ne sérüljön. Három helyzetben lehet egy csomópontot törölni a bináris keresési fából.
mikor találták fel az első számítógépet
A törlendő csomópont egy levélcsomópont
Ez a legegyszerűbb eset, ebben az esetben cserélje ki a levél csomópontját NULL-ra, és egyszerűen szabadítsa fel a lefoglalt helyet.
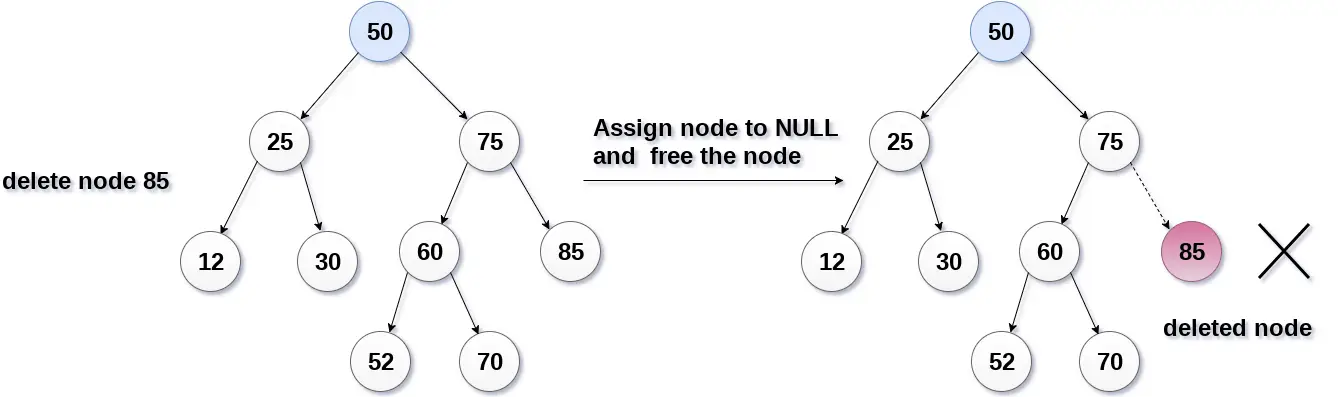
A következő képen a 85-ös csomópontot töröljük, mivel a csomópont egy levélcsomópont, ezért a csomópont NULL-ra cserélődik, és a lefoglalt hely felszabadul.
A törölni kívánt csomópontnak csak egy gyermeke van.
Ebben az esetben cserélje ki a csomópontot a gyermekére, és törölje a gyermek csomópontot, amely most tartalmazza a törölni kívánt értéket. Egyszerűen cserélje ki a NULL-ra, és szabadítsa fel a lefoglalt területet.
A következő képen a 12 csomópontot törölni kell. Csak egy gyereke van. A csomópont lecserélődik a gyermek csomópontra, és a lecserélt 12-es csomópont (amely most levélcsomópont) egyszerűen törlődik.

A törölni kívánt csomópontnak két gyermeke van.
Ez egy kicsit összetett eset a másik két esethez képest. A törölni kívánt csomópont azonban rekurzívan lecserélődik a sorrendben lévő utódjával vagy elődjével, amíg a (törölni kívánt) csomópont értéke fel nem kerül a fa levelére. Az eljárás után cserélje ki a csomópontot NULL-ra, és szabadítsa fel a lefoglalt területet.
A következő képen az 50-es csomópontot kell törölni, amely a fa gyökércsomópontja. Az alábbiakban megadott fa sorrendben történő bejárása.
6, 25, 30, 50, 52, 60, 70, 75.
cserélje ki az 50-et a sorrendben lévő 52-es utódjával. Most az 50 átkerül a fa levelére, amely egyszerűen törlődik.

Algoritmus
Törlés (TREE, ITEM)
Írja be, hogy 'cikk nem található a fában' ELSE IF ITEM DATA
Törlés (TREE->LEFT, ITEM)
EGYÉB HA TÉTEL > FA -> ADATOK
Törlés (FA -> JOBBRA, TÉTEL)
MÁS HA FA -> BAL ÉS FA -> JOBBRA
HŐMÉRSÉKLET BEÁLLÍTÁSA = Legnagyobb csomópont keresése (FA -> BAL)
FA BEÁLLÍTÁSA -> ADATOK = TEMP -> DATA
Törlés (FA -> BAL, HŐMÉRSÉKLET -> ADATOK)
MÁS
SET TEMP = FA
IF FA -> LEFT = NULL ÉS FA -> JOBBRA = NULL
FA BEÁLLÍTÁSA = NULL
ELSE IF FA -> LEFT != NULL
FA BEÁLLÍTÁSA = FA -> LEFT
MÁS
FA BEÁLLÍTÁSA = FA -> JOBBRA
[HA VÉGE]
SZABAD HŐM
[HA VÉGE]
Funkció:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 