A százalék a matematika alapvető fogalma, amely nemcsak a matematikában fontos, hanem mindennapi életünkben is. Segít a törtek és az arányok egyszerű kifejezésében, megkönnyítve ezen értékek összehasonlítását és megértését. Az egyik gyakori példa, amely sok forgatókönyvben előfordul, a 30 százalék kiszámítása, ezért ebben a cikkben megismerjük a 30 százalék fogalmát, megértjük a 100 30 százaléka, és a végén ismerje meg az alkalmazásokat és a következtetést.
Százalékok megértése
Mielőtt megismerkednénk a 100 30 százalékának kiszámításával, bizonyosodjunk meg arról, hogy jól ismerjük a százalékok fogalmát. A százalék a 100-ból egy arány vagy egy tört kifejezésének módja. A szimbólum '%' százalékot jelent, és a következőképpen jelenik meg: ' százalék .' A százalékokat általában értékek összehasonlítására és relatív állítások készítésére használják.
A 100 30%-át számoljuk
A 100 30 százalékának kiszámításához egy egyszerű folyamatot kell követnünk. Mivel a '30%' 100-ból 30-at jelent, törtként is kifejezhetjük: 30/100. A 100 30%-ának meghatározásához szorozzuk meg a 30/100-at 100-zal.
Bontsuk le a számítást lépésről lépésre
Megtanuljuk, hogyan kell kiszámítani a 100 30%-át néhány egyszerű lépés segítségével, amelyeket a következő sorokban ismertetünk.
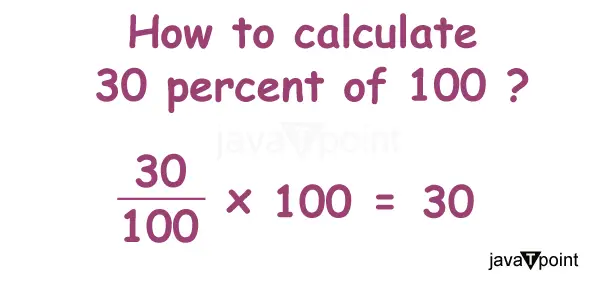
1. lépés . Először is írja fel mindkét szám szorzatát, azaz 30% és 100, az alábbiak szerint.
= 30% * 100
switch utasítás java
2. lépés . Mint tudjuk, a százalék jelentése a 100thegy szám egy részét vagy bármit, így a '%'-ot (1/100) helyettesíthetjük.
= 30% * 100 = (30/100) * 100
3. lépés . A szorzás és az egyszerűsítés szabályait felhasználva a következőket kapjuk:
=30% * 100 = (30/100) * 100
= 3000/100
= 30
Százalékok alkalmazásai
A következő beszélgetésben megismerjük néhány százalékos alkalmazást, amelyek valós példákhoz kapcsolódnak.
1. Vásárlási kedvezmények: Képzelje el, hogy felkeres egy üzletet, ahol 30 százalékos kedvezményt adnak egy 100 dolláros termékre. A megtakarított összeg kiszámításához meg kell határoznia a 100 dollár 30%-át. A számítás segítségével:
30/100 = 0,3
0,3 × 100 = 30
Ezért 30 dollárt takarít meg a 100 dolláros tételen; csak 70 dollárt kell fizetnie.
2. Vizsgapontszámok: Egy iskolában egy diák 100-ból 30 pontot ér el egy matematikai teszten. Az adott tanuló százalékos pontszámának meghatározásához ki kell számolnunk, hogy a 30 mekkora arányt képvisel a 100-ból. A képlet segítségével:
30/100 = 0,3
0,3 × 100 = 30%
Ezért a tanuló 30%-ot ért el a matematikai teszten.
3. Tőzsdei teljesítmény: Tegyük fel, hogy 100 dollárt fektet be egy részvénybe, és ez 30 százalékkal nő. A befektetés új értékének kiszámításához meg kell találnia a 100 dollár 30 százalékát. A fent leírt módszerrel:
30/100 = 0,3
0,3 × 100 = 30 USD
A részvény értéke 30 dollárral nőtt, így a befektetés értéke 130 dollár.
4. Valószínűség: A valószínűségszámításoknál százalékokat használnak; ha ma 35 százalék esély van az esőre, az azt jelenti, hogy minden 100 hasonló időjárási helyzetből 35-ben várható eső.
5. Statisztikai elemzés: A százalékokat széles körben használják a statisztikai elemzésben az adatok értelmezésére; segítenek az arányok összehasonlításában, a növekedési ütemek kiszámításában és az eloszlások megértésében.
Néhány megoldott példa
K. Mennyi a 10 30%-a?
Megoldás:
1. lépés: 30% * 10
2. lépés: 30% * 10 = (30/100) * 10
3. lépés: 30% * 10 = (30/100) * 10 = 300 / 100 = 3
K. Mennyi az 50 30%-a?
Megoldás:
1. lépés: 30% * 50
2. lépés: 30% * 50 = (30/100) * 50
3. lépés: 30% * 50 = (30/100) * 50 = 1500 / 100 = 15
K. Mennyi a 30 75%-a?
Megoldás:
1. lépés: 75% * 30
2. lépés: 75% * 30 = (75/100) * 30
3. lépés: 75% * 30 = (75/100) * 30 = 2250 / 100 = 22,5
K. Mennyi a 100 28%-a?
Megoldás:
1. lépés: 28% * 100
2. lépés: 28% * 100 = (28/100) * 100
3. lépés: 28% * 100 = (28/100) * 100 = 2800 / 100 = 28
K. Mennyi a 20 30%-a?
Megoldás:
1. lépés: 30% * 20
2. lépés: 30% * 20 = (30/100) * 20
3. lépés: 30% * 20 = (30/100) * 20 = 600 / 100 = 6
K. Mennyi a 200 30%-a?
Megoldás:
1. lépés: 30% * 200
2. lépés: 30% * 200 = (30/100) * 200
3. lépés: 30% * 200 = (30/100) * 200 = 6000 / 100 = 60
Következtetés
A százalékok a matematika egyik alapvető fogalma, amely lehetővé teszi az arányok kifejezését és az összehasonlításokat. Abban az esetben, ha a 100-ból 30%-ot számolunk, a teljes értéket megszorozzuk 30%-kal (0,3), hogy megkapjuk az eredményt, azaz 30-at. Ez a tudás megalapozott a matematikában, és alkalmazható különféle valós forgatókönyvekben, mint például eladások, hálapénz és pénzügyi befektetések. A százalékok és arányok megértésével fejleszthetjük problémamegoldó képességeinket, és megalapozott döntéseket hozhatunk az élet különböző területein.
