A PyTorch biztosítja a torch.nn modult, amely segít nekünk a neurális hálózat létrehozásában és betanításában. Először az alap neurális hálózatot fogjuk betanítani az MNIST adathalmazra anélkül, hogy ezekből a modellekből bármilyen funkciót használnánk. Csak az alapvető PyTorch tenzor funkciót fogjuk használni, majd fokozatosan hozzáadunk egy-egy funkciót a torch.nn fájlból.

A torch.nn számos további osztályt és modult biztosít számunkra a neurális hálózat megvalósításához és betanításához.

Az nn csomag a következő modulokat és osztályokat tartalmazza:

Igen nem	Osztály és modul	Leírás
1.	fáklya.nn.Paraméter	Ez egyfajta tenzor, amelyet modulparaméternek kell tekinteni.
2.	Konténerek
1) fáklya.nn.Modul	Ez egy alaposztály az összes neurális hálózati modulhoz.
2) fáklya.nn.Szekvenciális	Ez egy szekvenciális tároló, amelyben a modulok a konstruktorban való átadásuk sorrendjében kerülnek hozzáadásra.
3) torch.nn.ModuleList	Ez egy listában fogja tartani az almodulokat.
4) torch.nn.ModuleDict	Ez az almodulokat egy könyvtárban fogja tárolni.
5) torch.nn.ParameterList	Ez egy listában tartja a paramétereket.
6) torch.nn.parameterDict	Ez egy könyvtárban fogja tárolni a paramétereket.
3.	Konvolúciós rétegek
1) torch.nn.Conv1d	Ez a csomag 1D konvolúció alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
2) torch.nn.Conv2d	Ez a csomag 2D konvolúció alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
3) torch.nn.Conv3d	Ez a csomag 3D konvolúció alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
4) torch.nn.ConvTranspose1d	Ez a csomag egy 1D transzponált konvolúciós operátor alkalmazására szolgál több bemeneti síkból álló bemeneti képen.
5) torch.nn.ConvTranspose2d	Ez a csomag egy 2D transzponált konvolúciós operátor alkalmazására szolgál több bemeneti síkból álló bemeneti képen.
6) torch.nn.ConvTranspose3d	Ez a csomag egy 3D transzponált konvolúciós operátor alkalmazására szolgál több bemeneti síkból álló bemeneti képen.
7) fáklya.nn.Nyitja ki	Csúszó lokális blokkok kinyerésére szolgál egy kötegelt bemeneti tenzorból.
8) fáklya.nn.Fold	Csúszó lokális blokkok tömbjének egy nagy tartalmú tenzorba való kombinálására szolgál.
4.	A rétegek összevonása
1) zseblámpa.nn.MaxPool1d	1D max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
2) zseblámpa.nn.MaxPool2d	2D max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
3) torch.nn.MaxPool3d	3D max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
4) torch.nn.MaxUnpool1d	A MaxPool1d részleges inverzének kiszámítására szolgál.
5) torch.nn.MaxUnpool2d	A MaxPool2d részleges inverzének kiszámítására szolgál.
6) torch.nn.MaxUnpool3d	A MaxPool3d részleges inverzének kiszámítására szolgál.
7) torch.nn.AvgPool1d	Egy több bemeneti síkból álló bemeneti jelre 1D átlag pooling alkalmazására szolgál.
8) torch.nn.AvgPool2d	2D átlag pooling alkalmazására szolgál egy több bemeneti síkból álló bemeneti jelre.
9) torch.nn.AvgPool3d	Több bemeneti síkból álló bemeneti jelre 3D átlag pooling alkalmazására szolgál.
10) torch.nn.FractionalMaxPool2d	Egy több bemeneti síkból álló bemeneti jelre 2D-s tört max pooling alkalmazására szolgál.
11) fáklya.nn.LPPool1d	1D teljesítmény-átlag pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
12) torch.nn.LPPool2d	2D teljesítmény-átlag pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
13) torch.nn.AdavtiveMaxPool1d	1D adaptív max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
14) torch.nn.AdavtiveMaxPool2d	2D adaptív max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
15) torch.nn.AdavtiveMaxPool3d	3D adaptív max pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelen.
16) torch.nn.AdavtiveAvgPool1d	1D adaptív átlag pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelre.
17) torch.nn.AdavtiveAvgPool2d	2D adaptív átlag pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelre.
18) torch.nn.AdavtiveAvgPool3d	3D adaptív átlag pooling alkalmazására szolgál több bemeneti síkból álló bemeneti jelre.
5.	Párnázó rétegek
1) zseblámpa.nn.ReflectionPad1d	A bemeneti tenzort a bemeneti határ tükrözésével tölti fel.
2) zseblámpa.nn.ReflactionPad2d	A bemeneti tenzort a bemeneti határ tükrözésével tölti fel.
3) torch.nn.ReplicationPad1	Ez a bemeneti tenzort a bemeneti határ replikációjával tölti fel.
4) torch.nn.ReplicationPad2d	Ez a bemeneti tenzort a bemeneti határ replikációjával tölti fel.
5) torch.nn.ReplicationPad3d	Ez a bemeneti tenzort a bemeneti határ replikációjával tölti fel.
6) zseblámpa.nn.ZeroPad2d	A bemeneti tenzor határait nullával tölti fel.
7) torch.nn.ConstantPad1d	A bemeneti tenzor határait állandó értékkel tölti fel.
8) torch.nn.ConstantPad2d	A bemeneti tenzor határait állandó értékkel tölti fel.
9) torch.nn.ConstantPad3d	A bemeneti tenzor határait állandó értékkel tölti fel.
6.	Nemlineáris aktiválások (súlyozott összeg, nemlinearitás)
1) fáklya.nn.ELU	Ez az elemenkénti függvény alkalmazására szolgál: ELU(x)=max(0,x)+min(0,α*(exp(x)-1))
2) fáklya.nn.Hardshrink	A kemény zsugorodási funkció elemenkénti függvényének alkalmazására szolgál: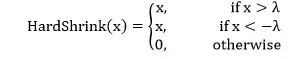
3) fáklya.nn.LeakyReLU	Ez az elemenkénti függvény alkalmazására szolgál: LeakyReLu(x)=max(0,x) +negatív_slope*min(0,x)
4) fáklya.nn.LogSigmoid	Ez az elemenkénti függvény alkalmazására szolgál:
5) fáklya.nn.MultiheadAttention	Arra használják, hogy lehetővé tegye a modell számára a különböző reprezentációs alterekből származó információk kezelését
6) fáklya.nn.PReLU	Az elemenkénti függvény alkalmazására lesz használva: PReLU(x)=max(0,x)+a*min(0,x)
7) fáklya.nn.ReLU	Az egyenirányított lineáris egység függvény elemenkénti alkalmazására szolgál: ReLU(x)=max(0,x)
8) fáklya.nn.ReLU6	Az elemenkénti függvény alkalmazására lesz használva: ReLU6(x)=min(max(0,x),6)
9) fáklya.nn.RReLU	A véletlenszerű szivárgó rektifikált lineáris egység függvény elemenkénti alkalmazására szolgál, a cikkben leírtak szerint:
10) fáklya.nn.SELU	Az elemenkénti függvényt a következőképpen alkalmazza: SELU(x)=skála*(max(0,x)+ min(0,a*(exp(x)-1))) Itt α= 1,6732632423543772848170429916717 és skála = 1,0507009873554804934193349852946.
11) fáklya.nn.TARGET	Az elemenkénti függvényt a következőképpen alkalmazza:
12) fáklya.nn.Sigmoid	Az elemenkénti függvényt a következőképpen alkalmazza:
13) zseblámpa.nn.Softplus	Az elemenkénti függvényt a következőképpen alkalmazza:
14) zseblámpa.nn.Lágyzsugor	A lágy zsugorodási funkció elemenkénti alkalmazására szolgál:
15) fáklya.nn.Softsign	Az elemenkénti függvényt a következőképpen alkalmazza:
16) fáklya.nn.Tanh	Az elemenkénti függvényt a következőképpen alkalmazza:
17) fáklya.nn.Tanhshrink	Az elemenkénti függvényt a következőképpen alkalmazza: Tanhzsugor(x)=x-Tanh(x)
18) fáklya.nn.Küszöb	A bemeneti tenzor minden elemének küszöbértékét fogja használni. A küszöb meghatározása a következő:
7.	Nemlineáris aktiválások (egyéb)
1) fáklya.nn.Softmin	A softmin függvény alkalmazására szolgál egy n-dimenziós bemeneti Tensorra, hogy átskálázza őket. Ezt követően az n-dimenziós kimeneti tenzor elemei a 0, 1 és 1 összegű tartományban vannak. A Softmin a következőképpen definiálható:
2) zseblámpa.nn.Softmax	A softmax függvény alkalmazására szolgál egy n-dimenziós bemeneti Tensorra, hogy átskálázza őket. Ezt követően az n-dimenziós kimeneti tenzor elemei a 0, 1 és 1 összegű tartományban vannak. A Softmax a következőképpen definiálható:
3) zseblámpa.nn.Softmax2d	SoftMax feletti jellemzők alkalmazására szolgál minden térbeli helyre.
4) zseblámpa.nn.LogSoftmax	A LogSoftmax függvény alkalmazására szolgál egy n-dimenziós bemeneti tenzorra. A LofSoftmax funkció a következőképpen definiálható:
5) torch.nn.AdaptiveLogSoftmaxWithLoss	Ez egy stratégia a nagy kimeneti terekkel rendelkező képzési modellekhez. Nagyon hatékony, ha a címkeeloszlás erősen kiegyensúlyozatlan
8.	Normalizációs rétegek
1) fáklya.nn.BatchNorm1d	2D vagy 3D bemenetek kötegelt normalizálására szolgál.
2) torch.nn.BatchNorm2d	A kötegelt normalizálás 4D-n keresztül történő alkalmazására szolgál.
3) torch.nn.BatchNorm3d	5D bemenetek kötegelt normalizálására szolgál.
4) fáklya.nn.GroupNorm	A csoport normalizálására szolgál a bemenetek mini kötegére.
5) torch.nn.SyncBatchNorm	Az n-dimenziós bemenetek kötegelt normalizálására szolgál.
6) torch.nn.InstanceNorm1d	Példánynormalizálás alkalmazására szolgál 3D bemeneten.
7) torch.nn.InstanceNorm2d	Példánynormalizálás alkalmazására szolgál 4D bemeneten.
8) torch.nn.InstanceNorm3d	Példánynormalizálás alkalmazására szolgál 5D bemeneten.
9) fáklya.nn.LayerNorm	A réteg normalizálására szolgál egy mini köteg bemeneten.
10) torch.nn.LocalResponseNorm	Helyi válasznormalizálásra szolgál egy több bemeneti síkból álló bemeneti jelen, ahol a csatorna a második dimenziót foglalja el.
9.	Ismétlődő rétegek
1) fáklya.nn.RNN	Többrétegű, tanh vagy ReLU nemlinearitású Elman RNN alkalmazására szolgál egy bemeneti szekvenciára. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez: ht=tanh(Wőketxt+bőket+Whhtt-1+bhh)
2) fáklya.nn.LSTM	Többrétegű hosszú rövid távú memória (LSTM) RNN alkalmazására szolgál egy bemeneti szekvenciára. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez:
3) fáklya.nn.GRU	Többrétegű kapuzott ismétlődő egység (GRU) RNN alkalmazására szolgál egy bemeneti sorozatra. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez:
4) fáklya.nn.RNNCell	Tanh vagy ReLU nemlinearitású Elman RNN cella bemeneti szekvenciára történő alkalmazására szolgál. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez: h'=tanh(Wőketx+bőket+Whhh+bhh) A Tanh helyett a ReLU használatos
5) fáklya.nn.LSTMCell	A hosszú rövid távú memória (LSTM) cella bemeneti szekvenciára való alkalmazására szolgál. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez: Ahol σ a szigmoid függvény, és * a Hadamard szorzat.
6) fáklya.nn.GRUCell	Egy kapuzott ismétlődő egység (GRU) cellának a bemeneti sorozatra történő alkalmazására szolgál. Minden réteg a következő függvényt számítja ki a beviteli sorozat minden eleméhez:
10.	Lineáris rétegek
1) fáklya.nn.Identitás	Ez egy helyőrző azonosító operátor, amely érzéketlen az argumentumokra.
2) fáklya.nn.Lineáris	A bejövő adatok lineáris transzformációjának alkalmazására szolgál: y=xAT+b
3) fáklya.nn.Bilineáris	A bejövő adatok bilineáris transzformációjának alkalmazására szolgál: y=x1Fejsze2+b
tizenegy.	Kieső rétegek
1) fáklya.nn.Lemorzsolódás	A neuronok koadaptációjának szabályozására és megelőzésére használják. Egy tényező edzés közben skálázza a kimenetet. Ez azt jelenti, hogy a modul kiszámol egy identitásfüggvényt a kiértékelés során.
2) fáklya.nn.Dropout2d	Ha a jellemzőtérképeken belül a szomszédos pixelek korrelálnak, akkor a torch.nn.Dropout nem szabályozza az aktiválásokat, és csökkenti a tényleges tanulási sebességet. Ebben az esetben a torch.nn.Dropout2d() a jellemzőtérképek közötti függetlenség elősegítésére szolgál.
3) torch.nn.Dropout3d	Ha a jellemzőtérképeken belül a szomszédos pixelek korrelálnak, akkor a torch.nn.Dropout nem szabályozza az aktiválásokat, és csökkenti a tényleges tanulási sebességet. Ebben az esetben a torch.nn.Dropout2d () a jellemzőtérképek közötti függetlenség elősegítésére szolgál.
4) fáklya.nn.AlphaDropout	Az Alpha Dropout alkalmazására szolgál a bemenetre. Az Alpha Dropout egy olyan típusú Dropout, amely fenntartja az önnormalizáló tulajdonságot.
12.	Ritka rétegek
1) fáklya.nn.Beágyazás	A szóbeágyazások tárolására és indexek segítségével történő lekérésére szolgál. A modul bemenete egy indexlista, a kimenet pedig a megfelelő szóbeágyazás.
2) fáklya.nn.EmbeddingBag	A beágyazás „zsákjainak” összegének vagy átlagának kiszámítására szolgál anélkül, hogy a közbenső beágyazást példányosítaná.
13.	Távolság funkció
1) fáklya.nn.KoszinuszHasonlóság	Visszaadja az x1 és x2 közötti koszinusz hasonlóságot, a dim mentén számítva.
2) fáklya.nn.PairwiseDistance	Kiszámítja a v1, v2 vektorok kötegenkénti páronkénti távolságát a p-norma segítségével:
14.	Veszteség funkció
1) fáklya.nn.L1Loss	Olyan kritériumhoz használják, amely az x bemenet egyes elemei és az y cél között méri az átlagos abszolút hibát. A nem csökkentett veszteség a következőképpen írható le: l(x,y)=L={l1,...,ln},ln=|xn-ésn|, Ahol N a köteg mérete.
2) fáklya.nn.MSELoss	Olyan kritériumhoz használják, amely az x bemenet egyes elemei és az y célpont közötti átlagos négyzetes hibát méri. A nem csökkentett veszteség a következőképpen írható le: l(x,y)=L={l1,...,ln},ln=(xn-ésn)2, Ahol N a köteg mérete.
3) fáklya.nn.CrossEntropyLoss	Ez a feltétel egyetlen osztályban egyesíti az nn.LogSoftmax() és nn.NLLLoss() függvényeket. Hasznos, ha egy osztályozási feladatot tanítunk C osztályokkal.
4) fáklya.nn.CTCLoss	A Connectionist Temporal Classification loss egy folyamatos idősor és egy célsorozat közötti veszteséget számítja ki.
5) fáklya.nn.NLLLoss	A negatív log-valószínűségi veszteség egy osztályozási probléma képzésére szolgál C osztályokkal.
6) fáklya.nn.PoissonNLLLoss	A negatív log-likelihood veszteség t Poisson-eloszlásával cél~Poisson(input)loss(input,target)=input-target*log(target!)he target.
7) fáklya.nn.KLDivLoss	Hasznos távolságmérték a folyamatos eloszlásnál, és akkor is hasznos, ha közvetlen regressziót végzünk a folytonos kimeneteloszlás terén.
8) fáklya.nn.BCELoss	Egy olyan kritérium létrehozására szolgál, amely a cél és a kimenet közötti bináris kereszt entrópiát méri. A nem csökkentett veszteség a következőképpen írható le: l(x,y)=L={l1,...,ln},ln=-vn[ésn*logxn+ (1-én)*log(1-xn)], Ahol N a köteg mérete.
9) torch.nn.BCEWithLogitsLoss	Egyetlen osztályban egyesíti a Sigmoid réteget és a BCELosst. A numerikus stabilitás érdekében kihasználhatjuk a log-sum-exp trükköt, ha a műveletet egy rétegbe egyesítjük.
10) torch.nn.MarginRankingLoss	Létrehoz egy kritériumot, amely méri az adott x1, x2 bemenetek veszteségét, két 1D mini-batch tenzort, és egy 1D mini-batch tenzor y címkét, amelyek 1-et vagy -1-et tartalmaznak. A veszteségfüggvény a mini-köteg minden egyes mintájánál a következő: veszteség(x,y)=max(0,-y*(x1-x2)+margó
11) torch.nn.HingeEmbeddingLoss	A HingeEmbeddingLoss egy adott x bemeneti tenzor és egy 1-et vagy -1-et tartalmazó y címkék tenzorának veszteségét méri. Annak mérésére szolgál, hogy két bemenet hasonló vagy eltérő. A veszteségfüggvény meghatározása a következő:
12) torch.nn.MultiLabelMarginLoss	Egy olyan kritérium létrehozására szolgál, amely optimalizálja a többosztályú, több osztályozású csuklóvesztést az x bemenet és az y kimenet között.
13) fáklya.nn.SmoothL1Loss	Olyan kritérium létrehozására szolgál, amely négyzetes tagot használ, ha az abszolút elemenkénti hiba 1 alá esik, egyébként pedig egy L1 tagot. Huber-vesztésként is ismert:
14) torch.nn.SoftMarginLoss	Egy olyan kritérium létrehozására szolgál, amely optimalizálja a kétosztályos besorolási logisztikai veszteséget az x bemeneti tenzor és y céltenzor között, amelyek 1-et vagy -1-et tartalmaznak.
15) torch.nn.MultiLabelSoftMarginLoss	Egy olyan kritérium létrehozására szolgál, amely optimalizálja a többcímkés egy-mindegyes veszteséget az x bemenet és a cél y (N, C) közötti max. entrópiája alapján.
16) torch.nn.CosinusEmbeddingLoss	Egy olyan kritérium létrehozására szolgál, amely az adott x1, x2 bemeneti tenzorok veszteségét méri, és egy y tenzorcímke 1 vagy -1 értékkel. A koszinusz távolság segítségével méri, hogy két bemenet hasonló-e vagy nem.
17) fáklya.nn.MultiMarginLoss	Egy olyan kritérium létrehozására szolgál, amely optimalizálja a többosztályos osztályozási csuklóvesztést az x bemenet és az y kimenet között.
18) torch.nn.TripletMarginLoss	Egy olyan kritérium létrehozására szolgál, amely egy adott x1, x2, x3 bemeneti tenzor és 0-nál nagyobb értékű margó tripletveszteségét méri. A minták közötti relatív hasonlóság mérésére szolgál. A triplett egy horgonyból, egy pozitív példából és egy negatív példából áll. L(a,p,n)=max{d(aén, pén)-d(aén,nén)+margó,0}
tizenöt.	Látásrétegek
1) torch.nn.PixelShuffle	Az elemek alaktenzorba rendezésére szolgál (*,C×r2,H,W) egy alaktenzorra (*,C,H×r,W,r)
2) fáklya.nn.Példa	Egy adott többcsatornás 1D, 2D vagy 3D adatok újramintavételezésére szolgál.
3) torch.nn.upsamplingNearest2d	A 2D legközelebbi szomszéd felmintavételezésének alkalmazására szolgál több bemeneti csatornából álló bemeneti jelre.
4) torch.nn.UpsamplingBilinear2d	2D bilineáris felmintavételezésre szolgál egy több bemeneti csatornából álló bemeneti jelre.
16.	DataParallel rétegek (több GPU, elosztott)
1) fáklya.nn.DataParallel	Az adatpárhuzamosság megvalósítására szolgál modulszinten.
2) torch.nn.DistributedDataParallel	Az elosztott adatpárhuzam megvalósítására szolgál, ami a torch.distributed csomagon alapul modul szinten.
3) torch.nn.DistributedDataParallelCPU	A CPU elosztott adatpárhuzamának megvalósítására szolgál modulszinten.
17.	segédprogramok
1) torch.nn.clip_grad_norm_	Egy iterálható paraméter gradiens normájának kivágására szolgál.
2) torch.nn.clip_grad_value_	A paraméterek iterálható gradiens normájának levágására szolgál a megadott értéknél.
3) torch.nn.parameters_to_vector	A paraméterek egy vektorba konvertálására szolgál.
4) torch.nn.vector_to_parameters	Egy vektor paraméterekké alakítására szolgál.
5) torch.nn.weight_norm	Arra szolgál, hogy súlynormalizálást alkalmazzon egy paraméterre az adott modulban.
6) torch.nn.remove_weight_norm	A súlynormalizálás és az újraparaméterezés eltávolítására szolgál egy modulból.
7) torch.nn.spectral_norm	Az adott modulban lévő paraméterek spektrális normalizálására szolgál.
8) torch.nn.PackedSequence	Ez egy csomagolt sorozat adatainak és batch_sizes listájának tárolására szolgál.
9) torch.nn.pack_padded_sequence	Változó hosszúságú párnázott szekvenciákat tartalmazó Tensor csomagolására szolgál.
10) torch.nn.pad_packed_sequence	Változó hosszúságú szekvenciák csomagolt kötegének kitöltésére szolgál.
11) torch.nn.pad_sequence	Változó hosszúságú tenzorok listájának kitöltésére szolgál kitöltési értékkel.
12) torch.nn.pack_sequence	Változó hosszúságú tenzorok listájának csomagolására szolgál
13) torch.nn.remove_spectral_norm	A spektrális normalizálás és az újraparaméterezés eltávolítására szolgál egy modulból.

Referencia:

https://pytorch.org/docs/stable/nn.html