Adva egy karakterláncot, keresse meg az adott karakterlánc bracket formában történő bontásának minden módját. Bezárja az egyes szubsztrákat zárójelbe.
java objektum egyenlőség
Példák:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Erősen javasoljuk, hogy minimalizálja a böngészőt, és először kipróbálja ezt.
Az ötlet a rekurzió használata. Két paramétert tartunk fenn - a következő feldolgozandó karakter és a kimeneti karakterlánc eddig. A következő karakter indexétől kezdjük, amelyet feldolgozunk, és a feldolgozatlan karakterláncmal kialakítva feldolgozható, a kimeneti karakterlánchoz, és a fennmaradó karakterláncon ismétlődik, amíg az egész karakterlánc feldolgozását feldolgozzuk. Az STD :: Substr segítségével a kimeneti karakterlánc kialakításához használjuk. Substr (POS N) az N hosszúságú szubsztringot adja vissza, amely az aktuális karakterlánc POS -ján kezdődik.
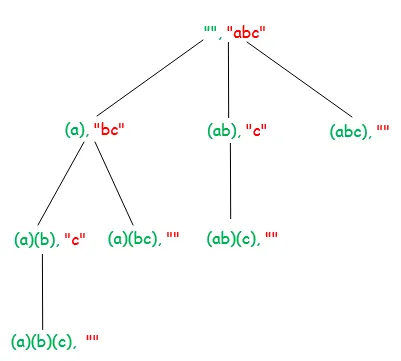
A diagram alatt az 'ABC' bemeneti karakterlánc rekurziós fát mutatja. Az ábra minden csomópontja a feldolgozott karakterláncot (zöld jelöléssel) és feldolgozatlan karakterláncot mutatja (piros jelölve).
mi az a hangszóró
Az alábbiakban bemutatjuk a fenti ötlet megvalósítását
C++// C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include
// Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations(String str int index String out) { if (index == str.length()) System.out.println(out); for (int i = index; i < str.length(); i++) // append substring formed by str[index // i] to output string findCombinations(str i + 1 out + '(' + str.substring(index i+1) + ')' ); } // Driver Code public static void main (String[] args) { // input string String str = 'abcd'; findCombinations(str 0 ''); } } // Contributed by Pramod Kumar
# Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations(string index out): if index == len(string): print(out) for i in range(index len(string) 1): # append substring formed by str[index # i] to output string findCombinations(string i + 1 out + '(' + string[index:i + 1] + ')') # Driver Code if __name__ == '__main__': # input string string = 'abcd' findCombinations(string 0 '') # This code is contributed by # sanjeev2552
// C# program to find all combinations // of Non-overlapping substrings formed // from given string using System; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations(string str int index string @out) { if (index == str.Length) { Console.WriteLine(@out); } for (int i = index; i < str.Length; i++) { // append substring formed by // str[index i] to output string findCombinations( str i + 1 @out + '(' + str.Substring(index (i + 1) - index) + ')'); } } // Driver Code public static void Main(string[] args) { // input string string str = 'abcd'; findCombinations(str 0 ''); } } // This code is contributed by Shrikant13
// Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations(string index out) { if (index == string.length) { console.log(out); } for (let i = index; i < string.length; i++) { // append substring formed by str[index // i] to output string findCombinations(string i + 1 out + '(' + string.substring(index i + 1) + ')'); } } // Driver Code const string = 'abcd'; findCombinations(string 0 ''); // contributed by adityasharmadev01
Kibocsátás
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Idő bonyolultsága: o (n2)
Kiegészítő tér: O (n2)
próbáld meg elkapni a java blokkot
