A lineáris regresszió és a logisztikai regresszió a két híres gépi tanulási algoritmus, amelyek felügyelt tanulási technikák alá tartoznak. Mivel mindkét algoritmus felügyelt jellegű, ezért ezek az algoritmusok címkézett adatkészletet használnak az előrejelzések elkészítéséhez. De a fő különbség köztük az, hogy hogyan használják őket. A lineáris regressziót a regressziós problémák megoldására, míg a logisztikus regressziót az osztályozási problémák megoldására használják. Az alábbiakban mindkét algoritmus leírását a különbségtáblázattal együtt adjuk meg.
Lineáris regresszió:
- A lineáris regresszió az egyik legegyszerűbb gépi tanulási algoritmus, amely a felügyelt tanulási technika alá tartozik, és regressziós problémák megoldására szolgál.
- A folytonos függő változó előrejelzésére szolgál független változók segítségével.
- A lineáris regresszió célja a legjobb illeszkedési vonal megtalálása, amely pontosan megjósolja a folytonos függő változó kimenetét.
- Ha egyetlen független változót használunk az előrejelzéshez, akkor egyszerű lineáris regressziónak nevezzük, és ha kettőnél több független változó van, akkor ezt a regressziót többszörös lineáris regressziónak nevezzük.
- A legjobb illeszkedési vonal megtalálásával az algoritmus megállapítja a kapcsolatot a függő változó és a független változó között. És a kapcsolatnak lineárisnak kell lennie.
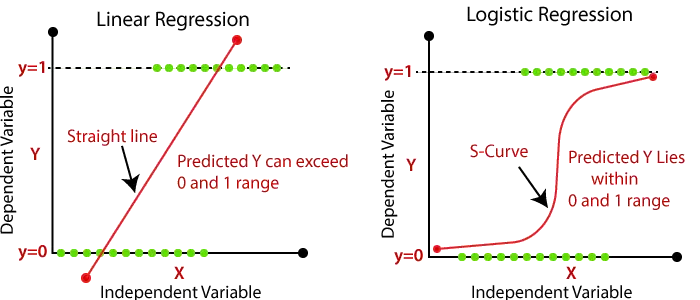
- A lineáris regresszió kimenete csak a folytonos értékek lehetnek, mint az ár, életkor, fizetés stb. A függő változó és a független változó közötti kapcsolat az alábbi képen látható:

A fenti képen a függő változó az Y tengelyen (fizetés) és a független változó az x tengelyen (tapasztalat) található. A regressziós egyenes a következőképpen írható fel:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Hol egy0és a1az együtthatók, ε pedig a hibatag.
Logisztikus regresszió:
- A logisztikai regresszió az egyik legnépszerűbb gépi tanulási algoritmus, amely a felügyelt tanulási technikák alá tartozik.
- Használható osztályozási és regressziós problémákra, de főleg osztályozási problémákra.
- Logisztikus regressziót használunk a kategorikus függő változó előrejelzésére független változók segítségével.
- A logisztikai regressziós probléma kimenete csak 0 és 1 között lehet.
- A logisztikus regresszió akkor használható, ha két osztály közötti valószínűségekre van szükség. Például hogy ma esik-e vagy sem, 0 vagy 1, igaz vagy hamis stb.
- A logisztikai regresszió a Maximum Likelihood becslés koncepcióján alapul. E becslés szerint a megfigyelt adatoknak a legvalószínűbbnek kell lenniük.
- A logisztikus regresszió során a bemenetek súlyozott összegét egy aktiváló függvényen keresztül adjuk át, amely 0 és 1 közötti értékeket tud leképezni. Az ilyen aktiválási függvény az úgynevezett szigmafunkció és a kapott görbét szigmoid görbének vagy S-görbének nevezzük. Vegye figyelembe az alábbi képet:

- A logisztikus regresszió egyenlete:

A lineáris regresszió és a logisztikai regresszió közötti különbség:
| Lineáris regresszió | Logisztikus regresszió |
|---|---|
| Lineáris regressziót használunk a folytonos függő változó előrejelzésére egy adott független változókészlet segítségével. | A logisztikai regressziót a kategorikus függő változó előrejelzésére használják egy adott független változókészlet segítségével. |
| A lineáris regressziót a regressziós probléma megoldására használják. | A logisztikus regressziót osztályozási problémák megoldására használják. |
| A Lineáris regresszióban a folytonos változók értékét jósoljuk meg. | A logisztikus regresszióban megjósoljuk a kategorikus változók értékeit. |
| A lineáris regresszióban megtaláljuk a legjobban illeszkedő egyenest, amellyel könnyen megjósolhatjuk a kimenetet. | A logisztikai regresszióban megtaláljuk az S-görbét, amely alapján osztályozhatjuk a mintákat. |
| A pontosság becslésére a legkisebb négyzetes becslési módszert használják. | A maximális valószínűség becslési módszert használják a pontosság becslésére. |
| A lineáris regresszió kimenetének folytonos értéknek kell lennie, például ár, életkor stb. | A logisztikai regresszió kimenetének kategorikus értéknek kell lennie, például 0 vagy 1, igen vagy nem stb. |
| A Lineáris regresszióban a függő változó és a független változó közötti kapcsolatnak lineárisnak kell lennie. | A logisztikus regresszióban nem szükséges, hogy a függő és a független változó között lineáris kapcsolat legyen. |
| Lineáris regresszióban a független változók között kollinearitás lehet. | A logisztikus regresszióban nem lehet kollinearitás a független változó között. |
