- A hegymászó algoritmus egy helyi keresési algoritmus, amely folyamatosan a növekvő magasság/érték irányába mozog, hogy megtalálja a hegy csúcsát vagy a probléma legjobb megoldását. Akkor fejeződik be, amikor elér egy csúcsértéket, ahol egyik szomszédnak sincs magasabb értéke.
- A hegymászó algoritmus egy olyan technika, amelyet a matematikai problémák optimalizálására használnak. A hegymászó algoritmus egyik széles körben tárgyalt példája a Traveling-salesman Problem, amelyben minimalizálnunk kell az eladó által megtett távolságot.
- Mohó helyi keresésnek is nevezik, mivel csak a jó közvetlen szomszéd államra néz, azon túl nem.
- A hegymászó algoritmus csomópontja két összetevőből áll, ezek az állapot és az érték.
- A hegymászást többnyire akkor használják, ha jó heurisztika áll rendelkezésre.
- Ebben az algoritmusban nem kell karbantartanunk és kezelnünk a keresési fát vagy gráfot, mivel az csak egyetlen aktuális állapotot tart meg.
A hegymászás jellemzői:
Íme a hegymászó algoritmus néhány fő jellemzője:
Állapottér diagram hegymászáshoz:
Az állapottér tájkép a hegymászó algoritmus grafikus ábrázolása, amely egy grafikont mutat az algoritmus különböző állapotai és a célfüggvény/költség között.
objektum átalakítása stringgé
Az Y tengelyen vettük azt a függvényt, amely lehet célfüggvény vagy költségfüggvény, az x tengelyen pedig állapotteret. Ha az Y-tengely függvénye költség, akkor a keresés célja a globális minimum és a lokális minimum megtalálása. Ha az Y tengely függvénye az Objektív függvény, akkor a keresés célja a globális maximum és a lokális maximum megtalálása.
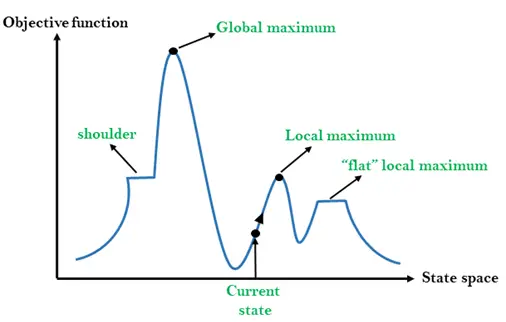
Az államtér tájának különböző régiói:
Helyi maximum: A lokális maximum egy olyan állapot, amely jobb, mint a szomszédos állapotok, de van egy másik állapot is, amely magasabb nála.
Globális maximum: A globális maximum az állapottér tájképének lehető legjobb állapota. Ennek a legmagasabb értéke a célfüggvény.
Jelen állapot: Ez egy olyan állapot a tájdiagramon, ahol egy ügynök jelenleg jelen van.
Lapos helyi maximum: Ez egy sík tér a tájban, ahol a jelenlegi állapotok összes szomszédos állama azonos értékű.
Váll: Ez egy fennsík régió, amely felfelé ível.
A hegymászó algoritmusok típusai:
- Egyszerű hegymászás:
- Legmeredekebb emelkedő hegymászás:
- Sztochasztikus hegymászás:
1. Egyszerű hegymászás:
Az egyszerű hegymászás a legegyszerűbb módja a hegymászó algoritmus megvalósításának. Egyszerre csak a szomszéd csomópont állapotát értékeli, és kiválasztja az elsőt, amely optimalizálja az aktuális költséget és beállítja aktuális állapotként . Csak azt ellenőrzi, hogy az egyik utódállapot-e, és ha jobbnak találja, mint a jelenlegi állapot, akkor mozgassa a másikat, hogy ugyanabban az állapotban legyen. Ez az algoritmus a következő tulajdonságokkal rendelkezik:
- Kevésbé időigényes
- Kevésbé optimális megoldás és a megoldás nem garantált
Algoritmus az egyszerű hegymászáshoz:
- Ha célállapot, akkor adja vissza a sikert és lépjen ki.
- Ellenkező esetben, ha jobb, mint a jelenlegi állapot, akkor rendeljen hozzá új állapotot aktuális állapotként.
- Ha nem jobb, mint a jelenlegi állapot, akkor térjen vissza a 2. lépéshez.
2. Legmeredekebb hegymászás:
A legmeredekebb-Emelkedés algoritmus az egyszerű hegymászó algoritmus egy változata. Ez az algoritmus megvizsgálja az aktuális állapot összes szomszédos csomópontját, és kiválaszt egy szomszédos csomópontot, amely a legközelebb van a célállapothoz. Ez az algoritmus több időt vesz igénybe, mivel több szomszédot keres
Algoritmus a legmeredekebb hegymászáshoz:
- Legyen a SUCC olyan állapot, amelynél a jelenlegi állapot bármely utódja jobb lesz nála.
- Minden egyes, az aktuális állapotra vonatkozó operátorhoz:
- Alkalmazza az új operátort, és hozzon létre egy új állapotot.
- Értékelje az új állapotot.
- Ha célállapot, akkor adja vissza, és lépjen ki, különben hasonlítsa össze a SUCC-vel.
- Ha jobb, mint a SUCC, akkor állítsa be az új állapotot SUCC-ként.
- Ha a SUCC jobb, mint az aktuális állapot, akkor állítsa az aktuális állapotot SUCC-ra.
3. Sztochasztikus hegymászás:
A sztochasztikus hegymászás nem vizsgálja meg minden szomszédját, mielőtt elindulna. Ez a keresési algoritmus inkább véletlenszerűen választ ki egy szomszédos csomópontot, és eldönti, hogy aktuális állapotként választja-e, vagy egy másik állapotot vizsgál.
Problémák a hegymászó algoritmusban:
1. Helyi maximum: A lokális maximum a táj azon csúcsállapota, amely minden szomszédos állapotánál jobb, de van egy másik állapot is, amely magasabb a lokális maximumnál.
Megoldás: A visszalépési technika a lokális maximum megoldása lehet az állapottérben. Hozzon létre egy listát az ígéretes útvonalról, hogy az algoritmus vissza tudjon lépni a keresési térben, és más útvonalakat is felfedezhessen.

2. fennsík: A plató a keresési tér azon sík területe, amelyben az aktuális állapot összes szomszédos állapota ugyanazt az értéket tartalmazza, mivel ez az algoritmus nem találja a legjobb mozgási irányt. A hegymászó keresés elveszhet a fennsík területén.
Megoldás: A plató megoldása a nagy vagy nagyon kis lépések keresése, a probléma megoldása. Véletlenszerűen válasszon egy olyan állapotot, amely messze van az aktuális állapottól, így lehetséges, hogy az algoritmus találhat nem fennsík régiót.

3. gerincek: A gerinc a helyi maximum speciális formája. Van egy területe, amely magasabb a környező területeinél, de maga lejtős, és nem érhető el egyetlen mozdulattal.
Megoldás: A kétirányú keresés használatával, vagy különböző irányú mozgással javíthatunk ezen a problémán.

Szimulált lágyítás:
Egy hegymászó algoritmus, amely soha nem lép fel alacsonyabb érték felé, garantáltan hiányos, mert megakadhat egy helyi maximumon. És ha az algoritmus véletlenszerű sétát alkalmaz egy utód mozgatásával, akkor az befejezheti, de nem hatékony. Szimulált lágyítás egy olyan algoritmus, amely egyszerre biztosítja a hatékonyságot és a teljességet.
betűméret latex
Mechanikai értelemben Lágyítás egy fém vagy üveg magas hőmérsékletre keményedésének, majd fokozatos lehűtésének folyamata, így a fém alacsony energiájú kristályos állapotot ér el. Ugyanezt a folyamatot használják a szimulált lágyításnál, amelyben az algoritmus véletlenszerű mozgást választ ki, ahelyett, hogy a legjobb lépést választaná. Ha a véletlenszerű mozgás javítja az állapotot, akkor ugyanazt az utat követi. Ellenkező esetben az algoritmus azt az utat követi, amelynek valószínűsége 1-nél kisebb, vagy lefelé haladva másik utat választ.
