Mi az a Heap?

A kupac egy teljes bináris fa, a bináris fa pedig olyan fa, amelyben a csomópontnak legfeljebb két gyermeke lehet. Mielőtt többet megtudna a kupacról Mi az a teljes bináris fa?

Egy teljes bináris fa a bináris fa, amelyben az utolsó szint, azaz a levél csomópont kivételével az összes szintet teljesen ki kell tölteni, és az összes csomópontot balra kell igazítani.

Értsük meg egy példán keresztül.

A fenti ábrán megfigyelhetjük, hogy a levélcsomópont kivételével az összes belső csomópont teljesen kitöltött; ezért azt mondhatjuk, hogy a fenti fa egy teljes bináris fa.

A fenti ábra azt mutatja, hogy a levélcsomópont kivételével az összes belső csomópont teljesen kitöltve van, de a levélcsomópontok a jobb oldalon vannak hozzáadva; ezért a fenti fa nem teljes bináris fa.

Megjegyzés: A kupacfa egy speciális kiegyensúlyozott bináris fa adatstruktúra, ahol a gyökércsomópontot összehasonlítják gyermekeivel, és ennek megfelelően rendezik el.

Hogyan rendezhetjük el a csomópontokat a fában?

Kétféle halom létezik:

• Min Heap
• Max kupac

Minimális kupac: A szülőcsomópont értékének kisebbnek kell lennie, vagy egyenlőnek kell lennie bármelyik gyermekével.

Vagy

Más szavakkal, a min-halom úgy definiálható, hogy minden i csomópontnál az i csomópont értéke nagyobb vagy egyenlő a szülőértékével, kivéve a gyökércsomópontot. Matematikailag a következőképpen definiálható:

A[szülő(i)]<= a[i]< strong>

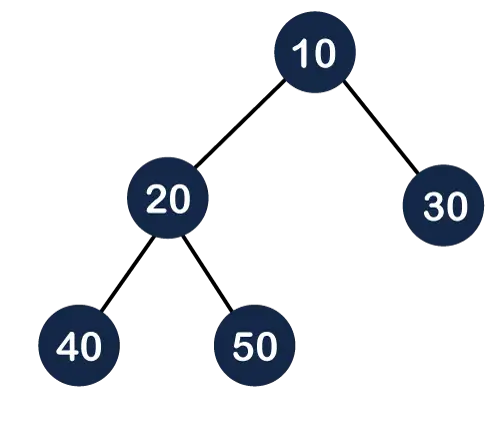
Értsük meg a min-halmot egy példán keresztül.

A fenti ábrán a 11 a gyökércsomópont, és a gyökércsomópont értéke kisebb, mint az összes többi csomópont értéke (bal oldali gyermek vagy jobb gyermek).

Max kupac: A szülőcsomópont értéke nagyobb vagy egyenlő, mint a gyermekei.

Vagy

Más szavakkal, a max kupac úgy definiálható, mint minden i csomópontnál; az i csomópont értéke kisebb vagy egyenlő a szülőértékével, kivéve a gyökércsomópontot. Matematikailag a következőképpen definiálható:

A[Szülő(i)] >= A[i]

A fenti fa egy max kupac fa, mivel kielégíti a max kupac tulajdonságát. Most pedig lássuk a max kupac tömbábrázolását.

Időbonyolítás a Max Heapben

A max kupacban szükséges összehasonlítások teljes száma a fa magasságától függ. A teljes bináris fa magassága mindig logn; ezért az időbonyolultság is O(logn) lenne.

A beszúrási művelet algoritmusa a max kupacban.

 // algorithm to insert an element in the max heap. insertHeap(A, n, value) { n=n+1; // n is incremented to insert the new element A[n]=value; // assign new value at the nth position i = n; // assign the value of n to i // loop will be executed until i becomes 1. while(i&gt;1) { parent= floor value of i/2; // Calculating the floor value of i/2 // Condition to check whether the value of parent is less than the given node or not if(A[parent] <a[i]) { swap(a[parent], a[i]); i="parent;" } else return; < pre> <p> <strong>Let&apos;s understand the max heap through an example</strong> .</p> <p>In the above figure, 55 is the parent node and it is greater than both of its child, and 11 is the parent of 9 and 8, so 11 is also greater than from both of its child. Therefore, we can say that the above tree is a max heap tree.</p> <p> <strong>Insertion in the Heap tree</strong> </p> <p> <strong>44, 33, 77, 11, 55, 88, 66</strong> </p> <p>Suppose we want to create the max heap tree. To create the max heap tree, we need to consider the following two cases:</p> <ul> <li>First, we have to insert the element in such a way that the property of the complete binary tree must be maintained.</li> <li>Secondly, the value of the parent node should be greater than the either of its child.</li> </ul> <p> <strong>Step 1:</strong> First we add the 44 element in the tree as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-5.webp" alt="Heap Data Structure"> <p> <strong>Step 2:</strong> The next element is 33. As we know that insertion in the binary tree always starts from the left side so 44 will be added at the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-6.webp" alt="Heap Data Structure"> <p> <strong>Step 3:</strong> The next element is 77 and it will be added to the right of the 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-7.webp" alt="Heap Data Structure"> <p>As we can observe in the above tree that it does not satisfy the max heap property, i.e., parent node 44 is less than the child 77. So, we will swap these two values as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-8.webp" alt="Heap Data Structure"> <p> <strong>Step 4:</strong> The next element is 11. The node 11 is added to the left of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-9.webp" alt="Heap Data Structure"> <p> <strong>Step 5:</strong> The next element is 55. To make it a complete binary tree, we will add the node 55 to the right of 33 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-10.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 33<55, so we will swap these two values as shown below:< p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-11.webp" alt="Heap Data Structure"> <p> <strong>Step 6:</strong> The next element is 88. The left subtree is completed so we will add 88 to the left of 44 as shown below:</p> <img src="//techcodeview.com/img/ds-tutorial/89/heap-data-structure-12.webp" alt="Heap Data Structure"> <p>As we can observe in the above figure that it does not satisfy the property of the max heap because 44<88, so we will swap these two values as shown below:< p> <p>Again, it is violating the max heap property because 88&gt;77 so we will swap these two values as shown below:</p> <p> <strong>Step 7:</strong> The next element is 66. To make a complete binary tree, we will add the 66 element to the right side of 77 as shown below:</p> <p>In the above figure, we can observe that the tree satisfies the property of max heap; therefore, it is a heap tree.</p> <p> <strong>Deletion in Heap Tree</strong> </p> <p>In Deletion in the heap tree, the root node is always deleted and it is replaced with the last element.</p> <p> <strong>Let&apos;s understand the deletion through an example.</strong> </p> <p> <strong>Step 1</strong> : In the above tree, the first 30 node is deleted from the tree and it is replaced with the 15 element as shown below:</p> <p>Now we will heapify the tree. We will check whether the 15 is greater than either of its child or not. 15 is less than 20 so we will swap these two values as shown below:</p> <p>Again, we will compare 15 with its child. Since 15 is greater than 10 so no swapping will occur.</p> <p> <strong>Algorithm to heapify the tree</strong> </p> <pre> MaxHeapify(A, n, i) { int largest =i; int l= 2i; int r= 2i+1; while(lA[largest]) { largest=l; } while(rA[largest]) { largest=r; } if(largest!=i) { swap(A[largest], A[i]); heapify(A, n, largest); }} </pre> <hr></88,></p></55,></p></a[i])>