A mohó módszer az egyik olyan stratégia, mint az Oszd meg és uralkodj a problémák megoldására. Ez a módszer az optimalizálási problémák megoldására szolgál. Az optimalizálási probléma olyan probléma, amely maximális vagy minimális eredményt igényel. Értsük meg néhány kifejezésen keresztül.
A Greedy módszer a legegyszerűbb és legegyszerűbb megközelítés. Ez nem egy algoritmus, hanem egy technika. Ennek a megközelítésnek a fő funkciója, hogy a döntést a jelenleg rendelkezésre álló információk alapján hozzák meg. Bármi legyen is a jelenlegi információ, a döntést anélkül hozzuk meg, hogy aggódnánk a jelenlegi döntés jövőbeli hatásai miatt.
java enums
Ezt a technikát alapvetően arra használják, hogy meghatározzák a megvalósítható megoldást, amely lehet vagy nem optimális. A megvalósítható megoldás egy olyan részhalmaz, amely megfelel a megadott kritériumoknak. Az optimális megoldás az a megoldás, amelyik a részhalmaz legjobb és legkedvezőbb megoldása. Megvalósítható esetben, ha több megoldás is megfelel a megadott kritériumoknak, akkor azokat a megoldásokat tekintjük megvalósíthatónak, míg az összes megoldás közül az optimális megoldás a legjobb megoldás.
A Greedy módszer jellemzői
A mohó módszer jellemzői a következők:
- A megoldás optimális felépítéséhez ez az algoritmus két halmazt hoz létre, ahol az egyik halmaz tartalmazza az összes kiválasztott elemet, a másik pedig az elutasított elemeket.
- A Greedy algoritmus jó helyi döntéseket hoz abban a reményben, hogy a megoldás megvalósítható vagy optimális lesz.
A mohó algoritmus összetevői
A mohó algoritmusban használható komponensek a következők:
aes vs des
A mohó algoritmus alkalmazásai
- A legrövidebb út megtalálására használják.
- A minimális feszítőfa megkeresésére szolgál a prím vagy a Kruskal-algoritmus segítségével.
- Határidős munkasorrendben használják.
- Ezt az algoritmust használják a tört hátizsák probléma megoldására is.
A Greedy Algorithm pszeudo kódja
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } A fenti a mohó algoritmus. Kezdetben a megoldás nulla értékkel van rendelve. A mohó algoritmusban átadjuk a tömböt és az elemek számát. A for cikluson belül egyenként kiválasztjuk az elemet, és ellenőrizzük, hogy a megoldás megvalósítható-e vagy sem. Ha a megoldás megvalósítható, akkor végrehajtjuk az egyesülést.
Értsük meg egy példán keresztül.
Tegyük fel, hogy 'P' probléma van. Szeretnék A-ból B-be utazni az alábbiak szerint:
P: A → B
A probléma az, hogy ezt az utat A-ból B-be kell utaznunk. A-ból B-be többféle megoldás létezik. A-ból B-be mehetünk úgy, hogy séta, autó, bicikli, vonat, repülőgép , stb. Az útnak van egy megkötése, hogy ezt az utat 12 órán belül meg kell utaznunk. Ha vonattal vagy repülővel megyek, akkor csak 12 órán belül tudom megtenni ezt a távolságot. Számos megoldás létezik erre a problémára, de csak két megoldás van, amely megfelel a megszorításnak.
Ha azt mondjuk, hogy minimális költséggel kell fedeznünk az utat. Ez azt jelenti, hogy ezt a távolságot a lehető legkevesebbet kell megtennünk, ezért ezt a problémát minimalizálási problémaként ismerjük. Eddig két megvalósítható megoldásunk van, az egyik vonattal, a másik légi úton. Mivel a vonatozás minimális költséggel jár, ezért ez egy optimális megoldás. Az optimális megoldás egyben a megvalósítható, de a legjobb eredményt nyújtó megoldás, hogy a megoldás legyen az optimális megoldás minimális költséggel. Egyetlen optimális megoldás lenne.
Azt a problémát, amelyhez minimális vagy maximális eredmény szükséges, ezt a problémát optimalizálási feladatnak nevezzük. A mohó módszer az optimalizálási problémák megoldására használt egyik stratégia.
tkinter gomb
A Greedy algoritmus használatának hátrányai
A mohó algoritmus az egyes fázisokban rendelkezésre álló információk alapján hoz döntéseket anélkül, hogy figyelembe venné a tágabb problémát. Így előfordulhat, hogy a mohó megoldás nem minden problémára adja a legjobb megoldást.
Minden szakaszban követi a helyi optimumot, azzal a szándékkal, hogy megtalálja a globális optimumot. Értsük meg egy példán keresztül.
Tekintsük az alábbi grafikont:
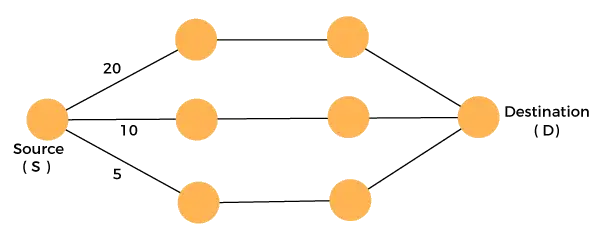
Minimális költséggel kell utaznunk a forrástól a célig. Mivel három megvalósítható megoldásunk van, amelyek költségútvonalai 10, 20 és 5, ezért az 5 a minimális költségút, így ez az optimális megoldás. Ez a lokális optimum, és így minden szakaszban megtaláljuk a lokális optimumot a globális optimális megoldás kiszámításához.
python // operátor
