A dinamikus programozás egy olyan technika, amely a problémákat részproblémákra bontja, és az eredményt elmenti jövőbeli célokra, hogy ne kelljen újra kiszámolnunk az eredményt. Az alproblémák az átfogó megoldás optimalizálására vannak optimalizálva, az úgynevezett optimális alépítménytulajdonság. A dinamikus programozás fő felhasználási területe az optimalizálási problémák megoldása. Itt az optimalizálási problémák azt jelentik, amikor egy probléma minimális vagy maximális megoldását próbáljuk megtalálni. A dinamikus programozás garantálja, hogy egy probléma optimális megoldását megtaláljuk, ha a megoldás létezik.
A dinamikus programozás definíciója szerint ez egy olyan technika, amely egy összetett probléma megoldására szolgál úgy, hogy először egyszerűbb részproblémák gyűjteményébe tör, minden részproblémát csak egyszer old meg, majd eltárolja a megoldásaikat az ismétlődő számítások elkerülése érdekében.
Értsük meg ezt a megközelítést egy példán keresztül.
Vegyünk egy példát a Fibonacci sorozatra. A következő sorozat a Fibonacci sorozat:
hegyesszög
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…
A fenti sorozatban szereplő számok nem véletlenszerűen vannak kiszámítva. Matematikailag mindegyik kifejezést felírhatjuk az alábbi képlettel:
F(n) = F(n-1) + F(n-2),
Az F(0) = 0 és F(1) = 1 alapértékekkel. A többi szám kiszámításához a fenti összefüggést követjük. Például F(2) az összeg f(0) és f(1), ami egyenlő 1-gyel.
Hogyan számíthatjuk ki az F(20)-t?
Az F(20) tagot a Fibonacci-sor n-edik képletével számítjuk ki. Az alábbi ábra bemutatja, hogyan kell kiszámítani az F(20) értéket.
szegmentációs hiba mag kidobva
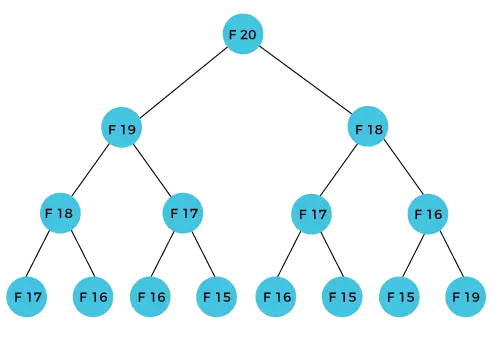
A fenti ábrán látható, hogy F(20) F(19) és F(18) összegeként kerül kiszámításra. A dinamikus programozási megközelítésben megpróbáljuk a problémát hasonló részproblémákra osztani. Ezt a megközelítést követjük a fenti esetben, ahol F(20) a hasonló részproblémákba, azaz F(19) és F(18). Ha összefoglaljuk a dinamikus programozás definícióját, az azt mondja, hogy a hasonló részproblémát nem szabad többször kiszámolni. Ennek ellenére a fenti esetben a részproblémát kétszer számítják ki. A fenti példában az F(18)-t kétszer számítjuk ki; hasonlóképpen az F(17) is kétszer kerül kiszámításra. Ez a technika azonban nagyon hasznos, mivel megoldja a hasonló részproblémákat, de óvatosnak kell lennünk az eredmények tárolásánál, mert nem foglalkozunk különösebben az egyszer kiszámított eredmény tárolásával, akkor az erőforrások pazarlásához vezethet.
A fenti példában, ha az F(18)-at a jobb oldali részfában számoljuk, akkor az hatalmas erőforrás-felhasználáshoz vezet, és csökkenti az általános teljesítményt.
A fenti probléma megoldása a kiszámított eredmények tömbben történő mentése. Először kiszámítjuk az F(16) és F(17) értékeket, és elmentjük az értékeket egy tömbbe. Az F(18) az F(17) és F(16) értékeinek összegzésével kerül kiszámításra, amelyek már el vannak mentve egy tömbben. Az F(18) kiszámított értéke egy tömbben kerül mentésre. Az F(19) értékét az F(18) és az F(17) összegéből számítjuk ki, és ezek értékei már el vannak mentve egy tömbben. Az F(19) számított értékét egy tömbben tároljuk. Az F(20) értéke F(19) és F(18) értékeinek összeadásával számítható ki, és mind az F(19) mind az F(18) értékeit egy tömbben tároljuk. Az F(20) végső számított értékét egy tömbben tároljuk.
Hogyan működik a dinamikus programozási megközelítés?
A dinamikus programozás lépései a következők:
- Az összetett problémát egyszerűbb részproblémákra bontja.
- Ezekre a részproblémákra megtalálja az optimális megoldást.
- Tárolja a részproblémák eredményeit (memoizáció). A részproblémák eredményeinek tárolásának folyamatát memorizálásnak nevezzük.
- Újra felhasználja őket, így ugyanaz a részprobléma többször kerül kiszámításra.
- Végül számítsa ki az összetett probléma eredményét.
A fenti öt lépés a dinamikus programozás alapvető lépései. A dinamikus programozás alkalmazható, amelyek olyan tulajdonságokkal rendelkeznek, mint:
kaptár építészet
Azok a problémák, amelyekben átfedő részproblémák és optimális alstruktúrák vannak. Itt az optimális alstruktúra azt jelenti, hogy az optimalizálási problémák megoldása az összes részprobléma optimális megoldásának egyszerű kombinálásával érhető el.
Dinamikus programozás esetén a köztes eredmények tárolásával a térkomplexitás nőne, de az időbonyolultság csökkenne.
miért változtathatatlan a string java-ban
A dinamikus programozás megközelítései
A dinamikus programozásnak két megközelítése van:
- Felülről lefelé irányuló megközelítés
- Alulról felfelé építkező megközelítés
Felülről lefelé irányuló megközelítés
A felülről lefelé irányuló megközelítés a memorizálási technikát, míg az alulról felfelé irányuló megközelítés a táblázatos módszert követi. Itt a memorizálás egyenlő a rekurzió és a gyorsítótárazás összegével. A rekurzió magának a függvénynek a meghívását jelenti, míg a gyorsítótárazás a köztes eredmények tárolását jelenti.
Előnyök
- Nagyon könnyen érthető és megvalósítható.
- Csak akkor oldja meg a részproblémákat, ha szükséges.
- Könnyű hibakeresés.
Hátrányok
A rekurziós technikát használja, amely több memóriát foglal el a hívási veremben. Néha, amikor a rekurzió túl mély, a verem túlcsordulási feltétele lép fel.
Több memóriát foglal el, ami rontja az általános teljesítményt.
Ismerjük meg a dinamikus programozást egy példán keresztül.
int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td> </tr><tr><td>Bottom-Up</td> </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let's understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let's understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>