Az Oszd meg és uralkodj egy algoritmikus minta. Algoritmikus módszereknél a tervezés lényege, hogy egy hatalmas bemeneten veszünk vitát, a bemenetet kisebb darabokra bontjuk, mindegyik kis darabon eldöntjük a problémát, majd egyesítjük a darabonkénti megoldásokat egy globális megoldásba. Ezt a problémamegoldó mechanizmust oszd meg és uralkodj stratégiának nevezzük.

Az Oszd meg és uralkodj algoritmus a következő három lépésből álló vitából áll.

Felosztaz eredeti problémát részproblémák halmazává.Meghódítani:Minden részproblémát egyenként, rekurzívan oldjon meg.Kombájn:Állítsa össze a részproblémák megoldásait, hogy megkapja az egész probléma megoldását.

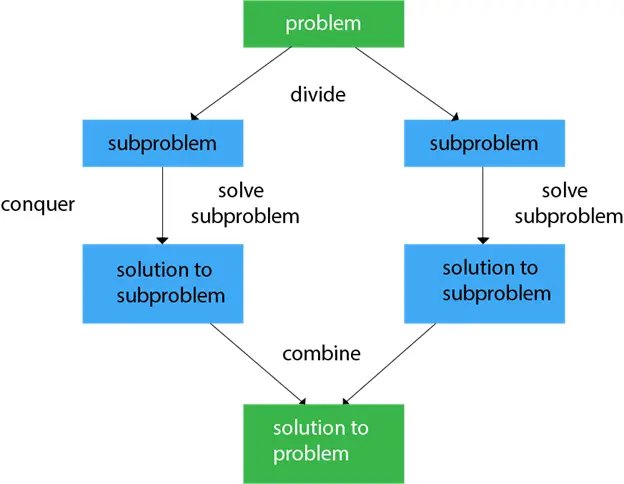
Általában követhetjük a Oszd meg és uralkodj háromlépcsős folyamatban történő megközelítés.

Példák: A konkrét számítógépes algoritmusok az Oszd meg és uralkodj megközelítésen alapulnak:

1. Maximum és Minimum probléma
2. Bináris keresés
3. Rendezés (egyesítés, gyors rendezés)
4. Hanoi tornya.

Az Oszd meg és uralkodj stratégia alapjai:

Az Oszd meg és uralkodj stratégiának két alapja van:

1. Relációs képlet
2. Leállási feltétel

1. Relációs képlet: Ez az a képlet, amelyet az adott technikából generálunk. A képlet generálása után alkalmazzuk a D&C stratégiát, azaz rekurzív módon megtörjük a problémát és megoldjuk a törött részproblémákat.

2. Leállási feltétel: Amikor a Divide & Conquer Stratégia segítségével megoldjuk a problémát, akkor tudnunk kell, hogy mennyi ideig kell alkalmazni az oszd meg és uralkodj. Tehát azt az állapotot, amikor a D&C rekurziós lépéseit le kell állítani, leállási feltételnek nevezzük.

Az oszd meg és uralkodj megközelítés alkalmazásai:

A következő algoritmusok az oszd meg és uralkodj technika elvén alapulnak:

Bináris keresés:A bináris keresési algoritmus egy keresési algoritmus, amelyet félintervallumú keresésnek vagy logaritmikus keresésnek is neveznek. Úgy működik, hogy összehasonlítja a célértéket a rendezett tömbben lévő középső elemmel. Az összehasonlítás után, ha az érték eltér, akkor a célt nem tartalmazó fele végül megszűnik, majd a másik felében folytatódik a keresés. Ismét figyelembe vesszük a középső elemet, és összehasonlítjuk a célértékkel. A folyamat addig ismétlődik, amíg el nem éri a célértéket. Ha a keresés befejezése után a másik felét üresnek találtuk, akkor megállapítható, hogy a cél nem szerepel a tömbben.Gyors rendezés:Ez a leghatékonyabb rendezési algoritmus, amelyet partíciócserés rendezésnek is neveznek. Először kiválaszt egy pivot értéket egy tömbből, majd a tömb többi elemét két altömbre osztja. A partíció úgy történik, hogy az egyes elemeket összehasonlítjuk a pivot értékkel. Összehasonlítja, hogy az elemnek nagyobb vagy kisebb értéke van-e, mint a pivot, majd rekurzívan rendezi a tömböket.Összevonási rendezés:Ez egy rendezési algoritmus, amely összehasonlítás alapján rendezi a tömböt. Úgy kezdődik, hogy egy tömböt altömbre oszt, majd mindegyiket rekurzívan rendezi. A rendezés végeztével visszaolvasztja őket.Legközelebbi pontpár:Ez a számítási geometria problémája. Ez az algoritmus a metrikus térben n pont adott legközelebbi pontpár meghatározására helyezi a hangsúlyt úgy, hogy a pontpárok közötti távolság minimális legyen.Strassen algoritmusa:Ez egy mátrixszorzási algoritmus, amely Volker Strassenről kapta a nevét. Sokkal gyorsabbnak bizonyult, mint a hagyományos algoritmus, amikor nagy mátrixokon dolgozik.Cooley-Tukey gyors Fourier transzformáció (FFT) algoritmus:A Fast Fourier Transform algoritmus J. W. Cooley és John Turkey nevéhez fűződik. Az oszd meg és uralkodj megközelítést követi, és az O(nlogn) összetettségét írja elő.Karatsuba algoritmus a gyors szorzáshoz:Ez a hagyományos idők egyik leggyorsabb szorzóalgoritmusa, Anatolij Karatsuba találta fel 1960 végén, és 1962-ben adták ki. Két n-jegyű számot szoroz meg oly módon, hogy legfeljebb egyjegyűre redukálja.

Az Oszd meg és uralkodj előnyei

• Az Oszd meg és uralkodj általában sikeresen megoldja az egyik legnagyobb problémát, például a Hanoi Towert, egy matematikai rejtvényt. Nehéz megoldani bonyolult problémákat, amelyekre nincs alapötlet, de az oszd meg és uralkodj megközelítés segítségével csökkentette a fáradságot, mivel a fő problémát két részre osztja, majd rekurzív módon oldja meg. Ez az algoritmus sokkal gyorsabb, mint a többi algoritmus.
• Hatékonyan használja a gyorsítótár memóriát anélkül, hogy sok helyet foglalna, mivel a lassabb főmemóriához való hozzáférés helyett egyszerű részproblémákat old meg a gyorsítótáron belül.
• Ez jártasabb, mint a megfelelő Brute Force technika.
• Mivel ezek az algoritmusok gátolják a párhuzamosságot, nem jár semmilyen módosítással, és párhuzamos feldolgozást alkalmazó rendszerek kezelik.

Az Oszd meg és uralkodj hátrányai

• Mivel a legtöbb algoritmusa rekurzió beépítésével készült, ezért nagy memóriakezelést tesz szükségessé.
• Egy explicit verem túlhasználhatja a helyet.
• Még a rendszer összeomlását is okozhatja, ha a rekurziót szigorúan nagyobb mértékben hajtják végre, mint a CPU-ban lévő verem.