
Adott a összekapcsolt irányítatlan gráf szomszédsági lista képviseli adjList[][] -vel n csomópontok és m élek, ahol minden csomópont rendelkezik a külön címke -tól 0-tól n-1-ig és minden adj[i] az i csúcshoz kapcsolódó csúcsok listáját jelenti.
Hozzon létre a klón ahol a gráf minden csomópontja tartalmaz egy egész számot val és egy tömb ( szomszédok ) csomópontok olyan csomópontokat tartalmaz, amelyek szomszédosak az aktuális csomóponttal.
js onclick
class Node {
val: egész szám
szomszédok: lista[csomópont]
}
Az Ön feladata az adott gráf klónozása és a klónozott gráf hivatkozásának visszaadása.
Jegyzet: Ha az adott gráf helyes másolatát adja vissza, a kimenet igaz lesz; ellenkező esetben, ha a másolat hibás, hamisan nyomtat.
karakterlánc
Példák
Bemenet: n = 4 adjList[][] = [[1 2] [0 2] [0 1 3] [2]]
Kimenet: igaz
Magyarázat:
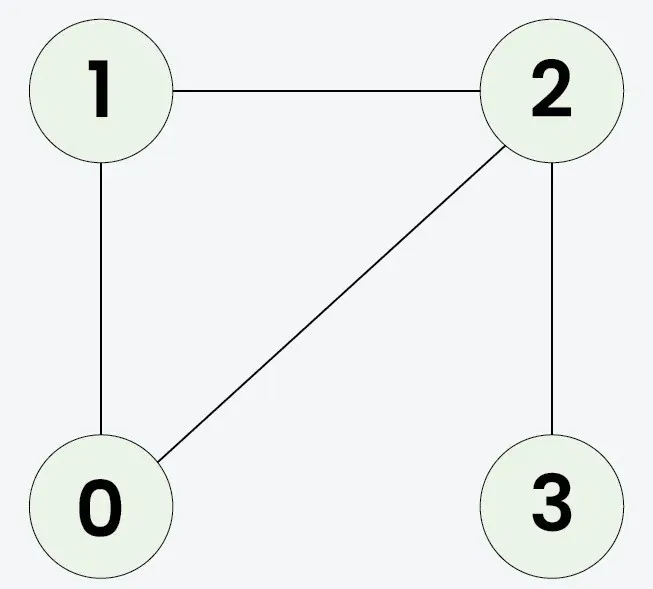
Mivel a klónozott gráf megegyezik az eredetivel, a kimenet igaz lesz.Bemenet: n = 3 adjList[][] = [[1 2] [0] [0]]
Kimenet: igaz
Magyarázat:
Mivel a klónozott gráf megegyezik az eredetivel, a kimenet igaz lesz.
Tartalomjegyzék
- Miért kell nyomon követnünk a meglátogatott/klónozott csomópontokat?
- Hogyan lehet nyomon követni a meglátogatott/klónozott csomópontokat?
- Hogyan lehet klón csomópontokat csatlakoztatni?
- Hogyan ellenőrizhető, hogy a klónozott gráf helyes-e?
- [1. megközelítés] BFS bejárás – O(V+E) idő és O(V) tér
- [2. megközelítés] DFS bejárás használata - O(V+E) idő és O(V) tér
Miért kell nyomon követnünk a meglátogatott/klónozott csomópontokat?
Követnünk kell a meglátogatott vagy klónozott csomópontokat, hogy elkerüljük a végtelen rekurziót és a redundáns munkát a gráf klónozása során. Mivel a gráfok tartalmazhatnak ciklusokat (ahol egy csomópont vissza tud mutatni egy korábban meglátogatott csomópontra), anélkül, hogy nyomon követnénk a már klónozott csomópontokat, a klónozási funkció vég nélkül meglátogatja ugyanazokat a csomópontokat, ami veremtúlcsordulást vagy helytelen duplikációt eredményez.
Hogyan lehet nyomon követni a meglátogatott/klónozott csomópontokat?
HashMap/Map szükséges az összes már létrehozott csomópont karbantartásához. Kulcsüzletek : Az eredeti csomópont hivatkozása/címe Értéktárak : A klónozott csomópont hivatkozása/címe A gráf összes csomópontjáról másolat készült.
Hogyan lehet klón csomópontokat csatlakoztatni?
A szomszédos csúcsok meglátogatása közben a csomópont be szerezze be a megfelelő klónozást csomópont mert hívjuk így IN most keresse fel az összes szomszédos csomópontot be és minden szomszédhoz keresse meg a megfelelő klón csomópontot (ha nem található, hozzon létre egyet), majd nyomja be a szomszédos vektorba IN csomópont.
hogyan kell végrehajtani egy szkriptet
Hogyan ellenőrizhető, hogy a klónozott gráf helyes-e?
Végezzen BFS bejárást az eredeti gráfon a klónozás előtt, majd a klónozás befejezése után ismét a klónozott gráfon. Minden bejárás során nyomtassa ki az egyes csomópontok értékét a címével (vagy hivatkozásával) együtt. A klónozás helyességének ellenőrzéséhez hasonlítsa össze a két bejárás során meglátogatott csomópontok sorrendjét. Ha a csomópontértékek ugyanabban a sorrendben jelennek meg, de a címeik (vagy hivatkozásaik) különböznek, akkor ez megerősíti, hogy a gráf sikeresen és helyesen klónozott.
Fedezze fel, hogyan irányítatlan gráf klónozása, amely több összekapcsolt komponenst tartalmazó gráfokat tartalmaz BFS vagy DFS használatával biztosítva az összes csomópont és él teljes mélymásolatát.
[1. megközelítés] BFS bejárás – O(V+E) idő és O(V) tér
C++A BFS-megközelítésben a gráfot iteratív módon klónozzuk egy sor segítségével. Kezdjük a kezdeti csomópont klónozásával és a sorba helyezésével. Ahogy feldolgozzuk a sor egyes csomópontjait, meglátogatjuk a szomszédokat. Ha egy szomszédot még nem klónoztunk, akkor létrehozunk egy klónt, amelyet egy térképen tárolunk, és sorba helyezzük későbbi feldolgozáshoz. Ezután hozzáadjuk a szomszéd klónját az aktuális csomópont klónjának szomszédok listájához. Ez a folyamat szintről szintre folytatódik, biztosítva, hogy az összes csomópont szélesség-első sorrendben kerüljön látogatásra. A BFS különösen hasznos a mély rekurzió elkerülésére és a nagy vagy széles grafikonok hatékony kezelésére.
#include
import java.util.*; // Definition for a Node class Node { public int val; public ArrayList<Node> neighbors; public Node() { neighbors = new ArrayList<>(); } public Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Clone the graph public static Node cloneGraph(Node node) { if (node == null) return null; Map<Node Node> mp = new HashMap<>(); Queue<Node> q = new LinkedList<>(); // Clone the starting node Node clone = new Node(node.val); mp.put(node clone); q.offer(node); while (!q.isEmpty()) { Node current = q.poll(); for (Node neighbor : current.neighbors) { // Clone neighbor if it hasn't been cloned yet if (!mp.containsKey(neighbor)) { mp.put(neighbor new Node(neighbor.val)); q.offer(neighbor); } // Add the clone of the neighbor to the current node's clone mp.get(current).neighbors.add(mp.get(neighbor)); } } return mp.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(new ArrayList<> (Arrays.asList(node2 node3))); node2.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node3))); node3.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node2 node4))); node4.neighbors.addAll(new ArrayList<> (Arrays.asList(node3))); return node1; } // Compare two graphs for structure and value public static boolean compareGraphs(Node n1 Node n2 HashMap<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || n1 == n2) return false; visited.put(n1 n2); if (n1.neighbors.size() != n2.neighbors.size()) return false; for (int i = 0; i < n1.neighbors.size(); i++) { Node neighbor1 = n1.neighbors.get(i); Node neighbor2 = n2.neighbors.get(i); if (visited.containsKey(neighbor1)) { if (visited.get(neighbor1) != neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void main(String[] args) { Node original = buildGraph(); Node cloned = cloneGraph(original); boolean isEqual = compareGraphs(original cloned new HashMap<>()); System.out.println(isEqual ? 'true' : 'false'); } }
from collections import deque # Definition for a Node class Node: def __init__(self val=0): self.val = val self.neighbors = [] # Clone the graph def cloneGraph(node): if not node: return None # Map to hold original nodes as keys and their clones as values mp = {} # Initialize BFS queue q = deque([node]) # Clone the starting node mp[node] = Node(node.val) while q: current = q.popleft() for neighbor in current.neighbors: # If neighbor not cloned yet if neighbor not in mp: mp[neighbor] = Node(neighbor.val) q.append(neighbor) # Link clone of neighbor to the clone of the current node mp[current].neighbors.append(mp[neighbor]) return mp[node] # Build graph def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs structurally and by values def compareGraphs(n1 n2 visited): if not n1 or not n2: return n1 == n2 if n1.val != n2.val or n1 is n2: return False visited[n1] = n2 if len(n1.neighbors) != len(n2.neighbors): return False for i in range(len(n1.neighbors)): neighbor1 = n1.neighbors[i] neighbor2 = n2.neighbors[i] if neighbor1 in visited: if visited[neighbor1] != neighbor2: return False else: if not compareGraphs(neighbor1 neighbor2 visited): return False return True # Driver if __name__ == '__main__': original = buildGraph() cloned = cloneGraph(original) result = compareGraphs(original cloned {}) print('true' if result else 'false')
using System; using System.Collections.Generic; // Definition for a Node public class Node { public int val; public List<Node> neighbors; public Node() { neighbors = new List<Node>(); } public Node(int val) { this.val = val; neighbors = new List<Node>(); } } class GfG { // Clone the graph public static Node CloneGraph(Node node) { if (node == null) return null; var mp = new Dictionary<Node Node>(); var q = new Queue<Node>(); // Clone the starting node var clone = new Node(node.val); mp[node] = clone; q.Enqueue(node); while (q.Count > 0) { var current = q.Dequeue(); foreach (var neighbor in current.neighbors) { // If neighbor not cloned clone it and enqueue if (!mp.ContainsKey(neighbor)) { mp[neighbor] = new Node(neighbor.val); q.Enqueue(neighbor); } // Add clone of neighbor to clone of current mp[current].neighbors.Add(mp[neighbor]); } } return mp[node]; } // Build graph public static Node BuildGraph() { var node1 = new Node(0); var node2 = new Node(1); var node3 = new Node(2); var node4 = new Node(3); node1.neighbors.AddRange(new[] { node2 node3 }); node2.neighbors.AddRange(new[] { node1 node3 }); node3.neighbors.AddRange(new[] { node1 node2 node4 }); node4.neighbors.AddRange(new[] { node3 }); return node1; } // Compare two graphs for structure and value public static bool CompareGraphs(Node n1 Node n2 Dictionary<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || ReferenceEquals(n1 n2)) return false; visited[n1] = n2; if (n1.neighbors.Count != n2.neighbors.Count) return false; for (int i = 0; i < n1.neighbors.Count; i++) { var neighbor1 = n1.neighbors[i]; var neighbor2 = n2.neighbors[i]; if (visited.ContainsKey(neighbor1)) { if (!ReferenceEquals(visited[neighbor1] neighbor2)) return false; } else { if (!CompareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void Main() { var original = BuildGraph(); var cloned = CloneGraph(original); var visited = new Dictionary<Node Node>(); Console.WriteLine(CompareGraphs(original cloned visited) ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Clone the graph function cloneGraph(node) { if (!node) return null; const mp = new Map(); const q = [node]; // Clone the initial node mp.set(node new Node(node.val)); while (q.length > 0) { const current = q.shift(); for (const neighbor of current.neighbors) { if (!mp.has(neighbor)) { mp.set(neighbor new Node(neighbor.val)); q.push(neighbor); } // Link clone of neighbor to clone of current mp.get(current).neighbors.push(mp.get(neighbor)); } } return mp.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors = [node2 node3]; node2.neighbors = [node1 node3]; node3.neighbors = [node1 node2 node4]; node4.neighbors = [node3]; return node1; } // Compare two graphs structurally and by value function compareGraphs(n1 n2 visited = new Map()) { if (!n1 || !n2) return n1 === n2; if (n1.val !== n2.val || n1 === n2) return false; visited.set(n1 n2); if (n1.neighbors.length !== n2.neighbors.length) return false; for (let i = 0; i < n1.neighbors.length; i++) { const neighbor1 = n1.neighbors[i]; const neighbor2 = n2.neighbors[i]; if (visited.has(neighbor1)) { if (visited.get(neighbor1) !== neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } // Driver const original = buildGraph(); const cloned = cloneGraph(original); const result = compareGraphs(original cloned); console.log(result ? 'true' : 'false');
Kimenet
true
[2. megközelítés] DFS bejárás használata - O(V+E) idő és O(V) tér
C++A DFS megközelítésben a gráfot rekurzió segítségével klónozzuk. Az adott csomópontból indulunk ki, és a visszalépés előtt minden ág mentén a lehető legmesszebbre járunk. Egy térkép (vagy szótár) a már klónozott csomópontok nyomon követésére szolgál, hogy elkerülje ugyanazon csomópont többszöri feldolgozását és a ciklusok kezelését. Amikor először találkozunk egy csomóponttal, klónt készítünk róla, és eltároljuk a térképen. Ezután az adott csomópont minden szomszédját rekurzívan klónozzuk, és hozzáadjuk a klónozott szomszédot az aktuális csomópont klónjához. Ez biztosítja, hogy az összes csomópontot alaposan meglátogassák a visszatérés előtt, és a gráf szerkezetét hűen másolja.
többszálú java-ban
#include
import java.util.*; // Definition for a Node class Node { int val; ArrayList<Node> neighbors; Node() { neighbors = new ArrayList<>(); } Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Map to hold original node to its copy static HashMap<Node Node> copies = new HashMap<>(); // Function to clone the graph using DFS public static Node cloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.containsKey(node)) { Node clone = new Node(node.val); copies.put(node clone); // Recursively clone neighbors for (Node neighbor : node.neighbors) { clone.neighbors.add(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(Arrays.asList(node2 node3)); node2.neighbors.addAll(Arrays.asList(node1 node3)); node3.neighbors.addAll(Arrays.asList(node1node2 node4)); node4.neighbors.addAll(Arrays.asList(node3)); return node1; } // Compare two graphs for structural and value equality public static boolean compareGraphs(Node node1 Node node2 HashMap<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited.put(node1 node2); if (node1.neighbors.size() != node2.neighbors.size()) return false; for (int i = 0; i < node1.neighbors.size(); i++) { Node n1 = node1.neighbors.get(i); Node n2 = node2.neighbors.get(i); if (visited.containsKey(n1)) { if (visited.get(n1) != n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void main(String[] args) { Node original = buildGraph(); // Clone the graph Node cloned = cloneGraph(original); // Compare original and cloned graph boolean result = compareGraphs(original cloned new HashMap<>()); System.out.println(result ? 'true' : 'false'); } }
# Definition for a Node class Node: def __init__(self val=0 neighbors=None): self.val = val self.neighbors = neighbors if neighbors is not None else [] # Map to hold original node to its copy copies = {} # Function to clone the graph def cloneGraph(node): # If the node is None return None if not node: return None # If node is not yet cloned clone it if node not in copies: # Create a clone of the node clone = Node(node.val) copies[node] = clone # Recursively clone neighbors for neighbor in node.neighbors: clone.neighbors.append(cloneGraph(neighbor)) # Return the clone return copies[node] def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs for structural and value equality def compareGraphs(node1 node2 visited): if not node1 or not node2: return node1 == node2 if node1.val != node2.val or node1 is node2: return False visited[node1] = node2 if len(node1.neighbors) != len(node2.neighbors): return False for i in range(len(node1.neighbors)): n1 = node1.neighbors[i] n2 = node2.neighbors[i] if n1 in visited: if visited[n1] != n2: return False else: if not compareGraphs(n1 n2 visited): return False return True # Driver Code if __name__ == '__main__': original = buildGraph() # Clone the graph using DFS cloned = cloneGraph(original) # Compare original and cloned graph visited = {} print('true' if compareGraphs(original cloned visited) else 'false')
using System; using System.Collections.Generic; public class Node { public int val; public List<Node> neighbors; public Node() { val = 0; neighbors = new List<Node>(); } public Node(int _val) { val = _val; neighbors = new List<Node>(); } } class GfG { // Dictionary to hold original node to its copy static Dictionary<Node Node> copies = new Dictionary<Node Node>(); // Function to clone the graph using DFS public static Node CloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.ContainsKey(node)) { Node clone = new Node(node.val); copies[node] = clone; // Recursively clone neighbors foreach (Node neighbor in node.neighbors) { clone.neighbors.Add(CloneGraph(neighbor)); } } // Return the clone return copies[node]; } // Build graph public static Node BuildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.Add(node2); node1.neighbors.Add(node3); node2.neighbors.Add(node1); node2.neighbors.Add(node3); node3.neighbors.Add(node1); node3.neighbors.Add(node2); node3.neighbors.Add(node4); node4.neighbors.Add(node3); return node1; } // Compare two graphs for structural and value equality public static bool CompareGraphs(Node node1 Node node2 Dictionary<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited[node1] = node2; if (node1.neighbors.Count != node2.neighbors.Count) return false; for (int i = 0; i < node1.neighbors.Count; i++) { Node n1 = node1.neighbors[i]; Node n2 = node2.neighbors[i]; if (visited.ContainsKey(n1)) { if (visited[n1] != n2) return false; } else { if (!CompareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void Main() { Node original = BuildGraph(); // Clone the graph using DFS Node cloned = CloneGraph(original); // Compare original and cloned graph bool isEqual = CompareGraphs(original cloned new Dictionary<Node Node>()); Console.WriteLine(isEqual ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Map to hold original node to its copy const copies = new Map(); // Function to clone the graph using DFS function cloneGraph(node) { // If the node is NULL return NULL if (node === null) return null; // If node is not yet cloned clone it if (!copies.has(node)) { const clone = new Node(node.val); copies.set(node clone); // Recursively clone neighbors for (let neighbor of node.neighbors) { clone.neighbors.push(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors.push(node2 node3); node2.neighbors.push(node1 node3); node3.neighbors.push(node1 node2 node4); node4.neighbors.push(node3); return node1; } // Compare two graphs for structural and value equality function compareGraphs(node1 node2 visited = new Map()) { if (!node1 || !node2) return node1 === node2; if (node1.val !== node2.val || node1 === node2) return false; visited.set(node1 node2); if (node1.neighbors.length !== node2.neighbors.length) return false; for (let i = 0; i < node1.neighbors.length; i++) { const n1 = node1.neighbors[i]; const n2 = node2.neighbors[i]; if (visited.has(n1)) { if (visited.get(n1) !== n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code const original = buildGraph(); // Clone the graph using DFS const cloned = cloneGraph(original); // Compare original and cloned graph console.log(compareGraphs(original cloned) ? 'true' : 'false');
Kimenet
true


