ELLENŐRIZZE, HOGY LÉTEZIK-E PONT A KÖR SZEKTORBAN VAGY SEM.

Van egy körünk, amelynek középpontja az origóban van (0 0). Bemenetként megadjuk a körszektor kezdőszögét és a körszektor méretét százalékban.

Példák:

Input : Radius = 8 StartAngle = 0 Percentage = 12 x = 3 y = 4 Output : Point (3 4) exists in the circle sector Input : Radius = 12 Startangle = 45 Percentage = 25 x = 3 y = 4 Output : Point (3 4) does not exist in the circle sector

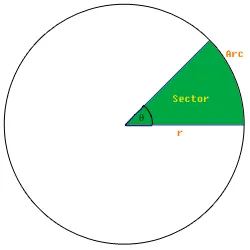Forrás: Wikibook.org

Ezen a képen a kezdőszög 0 fokos sugarú r, és tegyük fel, hogy a színes terület százaléka 12%, akkor a végszöget a következőképpen számítjuk ki 360/százalék + kezdőszög .

Annak megállapításához, hogy létezik-e egy pont (x y) egy kör szektorban (az origó közepén), megkeressük ennek a pontnak a polárkoordinátáit, majd a következő lépéseket hajtjuk végre:

Alakítsa át x y-t polárkoordinátákká ezzel
Szög = hiány(y/x); Sugár = sqrt(x * y y y y y y);
Ekkor a szögnek a kezdőszög és a végszög között, a sugárnak pedig 0 és a sugár között kell lennie.

C++

// C++ program to check if a point lies inside a circle // sector. #include   using namespace std; void checkPoint(int radius int x int y float percent  float startAngle) {  // calculate endAngle  float endAngle = 360/percent + startAngle;  // Calculate polar co-ordinates  float polarradius = sqrt(x*x+y*y);  float Angle = atan(y/x);  // Check whether polarradius is less then radius of circle  // or not and Angle is between startAngle and endAngle  // or not  if (Angle>=startAngle && Angle<=endAngle && polarradius<radius)  printf('Point (%d %d) exist in the circle sectorn' x y);  else  printf('Point (%d %d) does not exist in the circle sectorn'  x y); } // Driver code int main() {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle);  return 0; }

Java

// Java program to check if // a point lies inside a circle // sector. class GFG { static void checkPoint(int radius int x int y float percent  float startAngle) {  // calculate endAngle  float endAngle = 360/percent + startAngle;    // Calculate polar co-ordinates  double polarradius = Math.sqrt(x*x+y*y);  double Angle = Math.atan(y/x);    // Check whether polarradius is  // less then radius of circle  // or not and Angle is between  // startAngle and endAngle  // or not  if (Angle>=startAngle && Angle<=endAngle && polarradius<radius)  System.out.print('Point'+'('+x+''+y+')'+  ' exist in the circle sectorn');  else  System.out.print('Point'+'('+x+''+y+')'+  ' exist in the circle sectorn'); } // Driver Program to test above function public static void main(String arg[]) {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle); } } // This code is contributed // by Anant Agarwal.

Python3

# Python3 program to check if a point  # lies inside a circle sector. import math def checkPoint(radius x y percent startAngle): # calculate endAngle endAngle = 360 / percent + startAngle # Calculate polar co-ordinates polarradius = math.sqrt(x * x + y * y) Angle = math.atan(y / x) # Check whether polarradius is less # then radius of circle or not and  # Angle is between startAngle and  # endAngle or not if (Angle >= startAngle and Angle <= endAngle and polarradius < radius): print('Point (' x '' y ') ' 'exist in the circle sector') else: print('Point (' x '' y ') ' 'does not exist in the circle sector') # Driver code radius x y = 8 3 4 percent startAngle = 12 0 checkPoint(radius x y percent startAngle) # This code is contributed by # Smitha Dinesh Semwal

// C# program to check if a point lies // inside a circle sector. using System.IO; using System; class GFG {    static void checkPoint(int radius int x int y  float percent float startAngle)  {    // calculate endAngle  float endAngle = 360 / percent + startAngle;    // Calculate polar co-ordinates  float polarradius =   (float)Math.Sqrt(x * x + y * y);    float Angle = (float)Math.Atan(y / x);    // Check whether polarradius is less then   // radius of circle or not and Angle is   // between startAngle and endAngle or not  if (Angle >= startAngle && Angle <= endAngle  && polarradius < radius)  Console.Write('Point ({0} {1}) exist in '  + 'the circle sector' x y);  else  Console.Write('Point ({0} {1}) does not '  + 'exist in the circle sector' x y);  }    // Driver code  public static void Main()  {  int radius = 8 x = 3 y = 4;  float percent = 12 startAngle = 0;  checkPoint(radius x y percent startAngle);  } } // This code is contributed by Smitha Dinesh Semwal

JavaScript

<script> // Javascript program to check if // a point lies inside a circle // sector. function checkPoint(radius x y percent startAngle) {    // Calculate endAngle  let endAngle = 360 / percent + startAngle;    // Calculate polar co-ordinates  let polarradius = Math.sqrt(x * x + y * y);  let Angle = Math.atan(y / x);    // Check whether polarradius is  // less then radius of circle  // or not and Angle is between  // startAngle and endAngle  // or not  if (Angle >= startAngle &&   Angle <= endAngle &&   polarradius < radius)  document.write('Point' + '(' + x +   '' + y + ')' +  ' exist in the circle sectorn');  else  document.write('Point' + '(' + x +   '' + y + ')' +  ' exist in the circle sectorn'); }   // Driver code  let radius = 8 x = 3 y = 4; let percent = 12 startAngle = 0; checkPoint(radius x y percent startAngle); // This code is contributed by splevel62   </script>

Kimenet:

Point(3 4) exists in the circle sector

Időbeli összetettség: O(1)
Kiegészítő tér: O(1)

Kvíz létrehozása

TechCodeview

Ellenőrizze, hogy létezik-e pont a kör szektorban vagy sem.