A Bellman ford algoritmus egy forrásból álló legrövidebb út algoritmus. Ez az algoritmus arra szolgál, hogy megtalálja a legrövidebb távolságot az egyetlen csúcs és a súlyozott gráf összes többi csúcsa között. Számos más algoritmus is használható a legrövidebb út megtalálására, mint például a Dijkstra algoritmus stb. Ha a súlyozott gráf negatív súlyértékeket tartalmaz, akkor a Dijkstra algoritmus nem erősíti meg, hogy a helyes választ adja-e vagy sem. A Dijkstra algoritmussal ellentétben a bellman ford algoritmus akkor is garantálja a helyes választ, ha a súlyozott gráf negatív súlyértékeket tartalmaz.
Ennek az algoritmusnak a szabálya
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Tekintsük az alábbi grafikont:
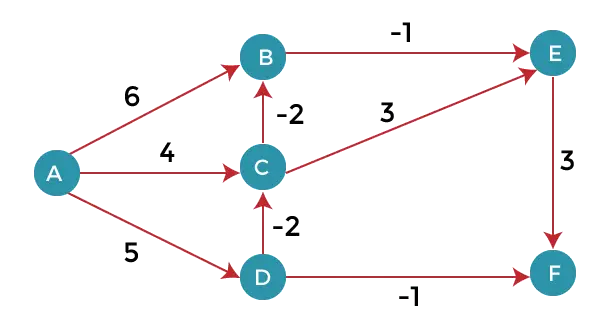
Amint azt a fenti grafikonon is láthatjuk, a súlyok egy része negatív. A fenti gráf 6 csúcsot tartalmaz, így tovább lazítunk az 5 csúcsig. Itt 5-ször lazítjuk meg az összes élt. A ciklus 5-ször ismétlődik, hogy megkapja a helyes választ. Ha a ciklust 5-nél többször iteráljuk, akkor a válasz is ugyanaz lesz, azaz nem változik a csúcsok közötti távolság.
A relaxáció azt jelenti:
c kód abs
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
Ezért a B csúcs távolsága 6.
Tekintsük az élt (A, C). Jelölje az 'A' csúcsot 'u'-val, a 'C' csúcsot 'v'-vel. Most használja a relaxációs formulát:
d(u) = 0
d(v) = ∞
c(u , v) = 4
Mivel (0 + 4) kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Ezért a C csúcs távolsága 4.
Tekintsük az élt (A, D). Az 'A' csúcsot 'u'-ként, a 'D' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
d(u) = 0
d(v) = ∞
c(u , v) = 5
Mivel (0 + 5) kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
Ezért a D csúcs távolsága 5.
Tekintsük az élt (B, E). Jelölje a 'B' csúcsot 'u'-val, az 'E' csúcsot pedig 'v'-vel. Most használja a relaxációs formulát:
d(u) = 6
d(v) = ∞
c(u , v) = -1
Mivel (6 - 1) kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 6 - 1 = 5
Ezért az E csúcs távolsága 5.
Tekintsük az élt (C, E). Jelölje a 'C' csúcsot 'u'-val, az 'E' csúcsot pedig 'v'-vel. Most használja a relaxációs formulát:
d(u) = 4
d(v) = 5
c(u , v) = 3
Mivel (4 + 3) nagyobb, mint 5, így nem lesz frissítés. Az E csúcs értéke 5.
Tekintsük az élt (D, C). A 'D' csúcsot 'u'-ként, a 'C' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
d(u) = 5
d(v) = 4
c(u , v) = -2
Mivel (5 -2) kisebb, mint 4, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 5-2 = 3
Ezért a C csúcs távolsága 3.
Tekintsük az élt (D, F). A 'D' csúcsot 'u'-ként, az 'F' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
d(u) = 5
d(v) = ∞
c(u , v) = -1
Mivel (5 -1) kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
Ezért az F csúcs távolsága 4.
Tekintsük az élt (E, F). Az 'E' csúcsot 'u'-val, az 'F' csúcsot 'v'-vel jelölje. Most használja a relaxációs formulát:
d(u) = 5
d(v) = ∞
c(u , v) = 3
Mivel (5 + 3) nagyobb, mint 4, így az F csúcs távolságértéke nem frissül.
Tekintsük az élt (C, B). A 'C' csúcsot 'u'-ként, a 'B' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
d(u) = 3
d(v) = 6
c(u , v) = -2
Mivel (3 - 2) kisebb, mint 6, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 3-2 = 1
Ezért a B csúcs távolsága 1.
Most az első iteráció befejeződött. Áttérünk a második iterációra.
Második iteráció:
tömb elemek hozzáadása java
A második iterációban ismét ellenőrizzük az összes élt. Az első él (A, B). Mivel (0 + 6) nagyobb, mint 1, így a B csúcsban nem történik frissítés.
A következő él (A, C). Mivel (0 + 4) nagyobb, mint 3, így a C csúcsban nem történik frissítés.
A következő él (A, D). Mivel (0 + 5) egyenlő 5-tel, így nem történik frissítés a D csúcsban.
A következő él (B, E). Mivel (1 - 1) egyenlő 0-val, ami kisebb, mint 5, ezért frissítse:
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B , E)
= 1-1 = 0
A következő él (C, E). Mivel (3 + 3) egyenlő 6-tal, ami nagyobb, mint 5, így az E csúcsban nem történik frissítés.
A következő él (D, C). Mivel (5 - 2) egyenlő 3-mal, így nem történik frissítés a C csúcsban.
A következő él (D, F). Mivel (5 - 1) egyenlő 4-gyel, így nem lesz frissítés az F csúcsban.
A következő él (E, F). Mivel (5 + 3) egyenlő 8-cal, ami nagyobb, mint 4, így az F csúcsban nem történik frissítés.
A következő él (C, B). Mivel a (3 - 2) egyenlő 1`-vel, így nem történik frissítés a B csúcsban.

Harmadik iteráció
Ugyanazokat a lépéseket hajtjuk végre, mint az előző iterációknál. Megfigyeljük, hogy a csúcsok távolságában nem lesz frissítés.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Idő összetettsége
A Bellman ford algoritmus időbonyolultsága O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
Ezért a 3. csúcs távolsága 5.
Tekintsük az élt (1, 2). Az '1' csúcsot 'u'-ként, a '2' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
d(u) = 0
d(v) = ∞
c(u , v) = 4
Mivel (0 + 4) kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Ezért a 2. csúcs távolsága 4.
Tekintsük az élt (3, 2). Jelölje a '3' csúcsot 'u'-val, a '2' csúcsot pedig 'v'-vel. Most használja a relaxációs formulát:
d(u) = 5
d(v) = 4
c(u , v) = 7
Mivel (5 + 7) nagyobb, mint 4, így a 2-es csúcsban nem lenne frissítés.
Tekintsük az élt (2, 4). A '2' csúcsot 'u'-ként, a '4' csúcsot 'v'-ként jelölje. Most használja a relaxációs formulát:
2-1 multiplexer
d(u) = 4
d(v) = ∞
c(u , v) = 7
Mivel (4 + 7) egyenlő 11-gyel, ami kisebb, mint ∞, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
Ezért a 4. csúcs távolsága 11.
Tekintsük az élt (4, 3). Jelölje a '4' csúcsot 'u'-val, a '3' csúcsot pedig 'v'-vel. Most használja a relaxációs formulát:
d(u) = 11
d(v) = 5
c(u , v) = -15
Mivel (11 - 15) egyenlő -4-gyel, ami kisebb, mint 5, ezért frissítse
d(v) = d(u) + c(u , v)
d(v) = 11-15 = -4
Ezért a 3. csúcs távolsága -4.
Most áttérünk a második iterációra.
Második iteráció
Most ismét ellenőrizzük az összes élt. Az első él (1, 3). Mivel (0 + 5) egyenlő 5-tel, ami nagyobb, mint -4, így nem történik frissítés a 3-as csúcsban.
A következő él az (1, 2). Mivel (0 + 4) egyenlő 4-gyel, így a 2-es csúcsban nem történik frissítés.
A következő él a (3, 2). Mivel (-4 + 7) egyenlő 3-mal, ami kisebb, mint 4, ezért frissítse:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Ezért a 2. csúcsban az érték 3.
A következő él a (2, 4). Mivel a ( 3+7) egyenlő 10-el, ami kevesebb, mint 11, ezért frissítsd
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Ezért a 4-es csúcson lévő érték 10.
pd egyesítés
A következő él a (4, 3). Mivel (10-15) egyenlő -5-tel, ami kisebb, mint -4, ezért frissítse:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Ezért a 3. csúcson lévő érték -5.
Most áttérünk a harmadik iterációra.
Harmadik iteráció
Most ismét ellenőrizzük az összes élt. Az első él (1, 3). Mivel (0 + 5) egyenlő 5-tel, ami nagyobb, mint -5, így nem történik frissítés a 3-as csúcsban.
A következő él az (1, 2). Mivel (0 + 4) egyenlő 4-gyel, ami nagyobb, mint 3, így a 2-es csúcsban nem történik frissítés.
A következő él a (3, 2). Mivel (-5 + 7) egyenlő 2-vel, ami kisebb, mint 3, ezért frissítse:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Ezért a 2-es csúcson lévő érték 2.
A következő él a (2, 4). Mivel (2 + 7) egyenlő 9-cel, ami kisebb, mint 10, ezért frissítse:
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Ezért a 4-es csúcs értéke 9.
A következő él a (4, 3). Mivel (9 - 15) egyenlő -6-tal, ami kisebb, mint -5, ezért frissítse:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Ezért a 3. csúcson lévő érték -6.

Mivel a gráf 4 csúcsot tartalmaz, így a bellman ford algoritmus szerint csak 3 iteráció lenne. Ha megpróbáljuk végrehajtani a 4thiteráció a gráfon, a csúcsok távolsága az adott csúcstól nem változhat. Ha a távolság változik, az azt jelenti, hogy a bellman ford algoritmus nem ad helyes választ.
4thismétlés
Az első él (1, 3). Mivel (0 +5) egyenlő 5-tel, ami nagyobb, mint -6, így a 3-as csúcs nem változna.
A következő él az (1, 2). Mivel (0 + 4) nagyobb, mint 2, így nem lesz frissítés.
A következő él a (3, 2). Mivel (-6 + 7) egyenlő 1-gyel, ami kisebb, mint 3, ezért frissítse:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
Ebben az esetben a csúcsérték frissül. Tehát arra a következtetésre jutottunk, hogy a bellman ford algoritmus nem működik, ha a grafikon tartalmazza a negatív súlyciklust.
Ezért a 2. csúcsban az érték 1.
